GRAFOS: Guía-> Recorridos, Profundidad, Anchura y Más

En los grafos el recorrido juega un papel crucial al permitirnos explorar y analizar conexiones entre nodos de manera sistemática.
A lo largo de esta lectura, desglosaremos cada aspecto relevante, proporcionando detalles exhaustivos y ejemplos con el fin de sumergirnos profundamente en este concepto.
- ¿Qué es un grafo?
- ¿Qué es el Recorrido en Grafos?
- Aplicaciones de los Grafos en la Vida Real
- Representación de los Grafos
- Tipos de Recorridos en Grafos
- Recorrido en Anchura (BFS)
- Recorrido en Profundidad (DFS)
- Comparación entre BFS y DFS
- Implementación de Recorridos en Lenguajes de Programación
- Recorridos en Grafos con Java
- Recorridos en Grafos con C++
- Recorridos en Grafos con JavaScript
- Comparación de Implementaciones entre Lenguajes
- Herramientas y Librerías para Grafos
- Caminos, Ciclos y Árboles en Grafos
- ¿Qué es un Grafo Euleriano?
- ¿Qué es un Grafo Hamiltoniano?
- Diferencias entre Grafos Eulerianos y Hamiltonianos
- Ejemplos de Grafos Hamiltonianos y Eulerianos
- Aplicaciones de los Grafos Eulerianos
- Aplicaciones de los Grafos Hamiltonianos
- Cómo Identificar un Grafo Euleriano
- Cómo Identificar un Grafo Hamiltoniano
- Algoritmos para Ciclos Eulerianos
- Algoritmos para Ciclos Hamiltonianos
- Algoritmos de Recorridos de Grafos Más Conocidos
- Grafos Ponderados y Grafos con Pesos Negativos
- Recorridos Especializados en Grafos Específicos
- Recorridos en Grafos Conexos y Dirigidos Acíclicos (DAG)
- Optimización de Recorridos en Grafos
- Evitar Nodos Repetidos y Mejorar la Eficiencia
- Que son los grafos en programacion
- Recorridos Avanzados y Modificados
- Desafíos en Grafos Muy Grandes
- Heurísticas y Recorridos A* en Grafos**
¿Qué es un grafo?
Un grafo es una estructura matemática que se utiliza para representar relaciones o conexiones entre distintos objetos. En términos formales, un grafo está compuesto por un conjunto de vértices (también llamados nodos) y un conjunto de aristas de un grafo(o enlaces) que conectan estos vértices. Esta estructura es fundamental en diversas áreas de la informática, especialmente en el campo de los algoritmos y en la teoría de redes.
Los grafos permiten modelar sistemas complejos, como redes sociales, sistemas de transporte, o incluso circuitos electrónicos. Al representar un sistema como un grafo, es posible estudiar su comportamiento y analizar sus propiedades de manera más eficiente.
Un grafo es una herramienta poderosa para representar situaciones donde hay conexiones entre elementos, facilitando la resolución de problemas relacionados con la interconectividad.
Definición básica de vértices y aristas
Los componentes principales de un grafo son los vértices y las aristas. Estos términos son clave para entender cómo funciona un grafo y cómo se puede utilizar en la práctica.
- Vértices: Representan los nodos o puntos en el grafo. Cada vértice puede estar conectado a otros vértices mediante aristas.
- Aristas: Las conexiones que unen los vértices. Estas pueden tener una dirección (en el caso de grafos dirigidos) o no (en grafos no dirigidos).
Por ejemplo, si quisiéramos representar un mapa de ciudades como un grafo, las ciudades serían los vértices y las carreteras que conectan las ciudades serían las aristas. Cada arista podría tener una longitud asociada, representando la distancia entre las ciudades.
Diferencias entre grafos dirigidos y no dirigidos
Una de las principales clasificaciones de los grafos es si son dirigidos o no dirigidos. Esta distinción es fundamental para entender cómo se comportan las conexiones entre los vértices en diferentes tipos de grafos.
- Grafo dirigido: En un grafo dirigido, las aristas tienen una dirección. Esto significa que si existe una arista entre los vértices A y B, se puede ir de A a B, pero no necesariamente de B a A.
- Grafo no dirigido: En los grafos no dirigidos, las aristas no tienen dirección, es decir, si existe una conexión entre A y B, se puede viajar en ambas direcciones, de A a B y de B a A.
La siguiente tabla resume las diferencias entre ambos tipos de grafo dirigido y no dirigido:
| Característica | Grafo dirigido | Grafo no dirigido |
|---|---|---|
| Dirección de las aristas | Las aristas tienen dirección (A → B) | Las aristas no tienen dirección (A ↔ B) |
| Aplicaciones comunes | Redes de tráfico, redes de flujo | Redes sociales, circuitos eléctricos |
| Representación en algoritmos | Algoritmos específicos para tratar direcciones | Algoritmos más sencillos en términos de conectividad |
Ambos tipos de grafos tienen sus ventajas y aplicaciones dependiendo del contexto en que se utilicen. En la práctica, los grafos dirigidos se emplean en casos donde el sentido de las conexiones es importante, mientras que los grafos no dirigidos son más comunes en situaciones donde las conexiones son simétricas.
Representaciones de los grafos en la memoria (listas de adyacencia, matrices de adyacencia)
Los grafos pueden representarse en la memoria de un ordenador de diferentes formas, siendo las más comunes la lista de adyacencia y la matriz de adyacencia. La elección entre estas representaciones depende de factores como el tamaño del grafo y la densidad de las conexiones entre vértices.
Lista de adyacencia
Una lista de adyacencia almacena, para cada vértice, una lista de los vértices a los que está conectado. Esta representación es muy eficiente en términos de espacio, especialmente cuando el grafo es esparso (es decir, cuando hay pocas conexiones en relación al número de vértices).
- Ventajas:
- Utiliza menos memoria en grafos con pocas aristas.
- Es eficiente para recorrer grafos esparsos.
- Desventajas:
- Puede ser más lenta para realizar ciertas operaciones, como comprobar si existe una conexión entre dos vértices específicos.
Matriz de adyacencia
La matriz de adyacencia es una tabla bidimensional donde las filas y las columnas representan los vértices del grafo, y el valor en la intersección de una fila y una columna indica si existe una arista entre esos vértices. Esta representación es útil cuando el grafo es denso (es decir, cuando la mayoría de los vértices están conectados entre sí).
- Ventajas:
- Es muy eficiente para comprobar si dos vértices están conectados.
- Facilita ciertas operaciones algorítmicas, como el cálculo de caminos mínimos.
- Desventajas:
- Consume más memoria, especialmente en grafos esparsos.
- Es menos eficiente para recorrer todos los vecinos de un vértice.
La siguiente tabla muestra una comparativa entre las listas y las matrices de adyacencia:
| Característica | Lista de adyacencia | Matriz de adyacencia |
|---|---|---|
| Espacio utilizado | Proporcional al número de aristas | Proporcional al cuadrado del número de vértices |
| Eficiencia en grafos esparsos | Muy eficiente | No tan eficiente |
| Eficiencia en grafos densos | Menos eficiente | Muy eficiente |
| Comprobación de conexiones | Menos eficiente | Muy rápida |
La elección entre lista de adyacencia y matriz de adyacencia depende del tipo de grafo que se esté utilizando y de las operaciones que se quieran realizar con mayor frecuencia.
¿Qué es el Recorrido en Grafos?
El recorrido en grafos es un concepto fundamental en la teoría de grafos, una rama de las matemáticas que estudia las relaciones entre nodos a través de conexiones llamadas aristas.
En términos simples, se refiere a seguir un camino específico dentro de un grafo, visitando cada nodo exactamente una vez.
Este proceso revela valiosa información sobre la estructura y conectividad del grafo en cuestión.
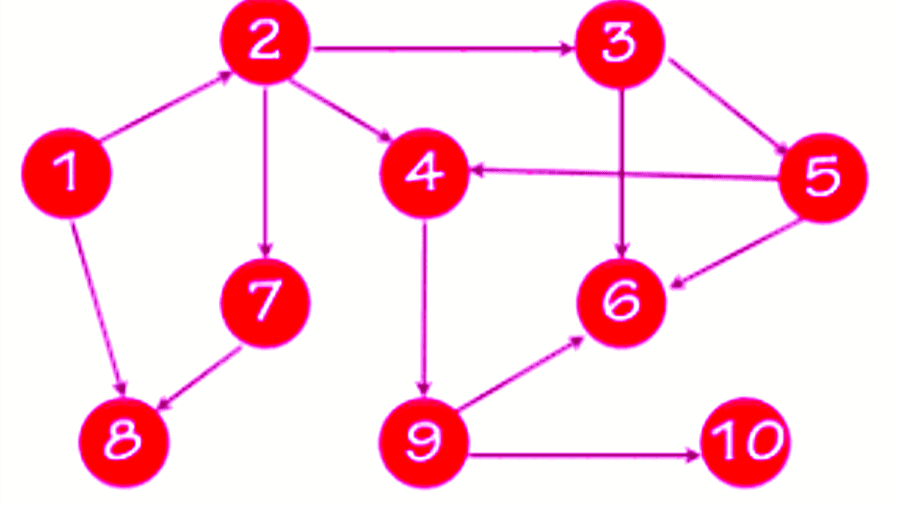
Para qué sirve
El recorrido en grafos sirve para:
- Analizar la conectividad entre nodos.
- Encontrar caminos específicos dentro de una red.
- Resolver problemas de optimización en diversas disciplinas.
- Modelar y entender sistemas complejos.
Para ilustrar su utilidad, imaginemos un grafo que representa una red de carreteras.
El recorrido en grafos nos permitiría encontrar la ruta más corta entre dos ubicaciones, lo que tiene aplicaciones directas en logística y planificación de rutas.

Aplicaciones de los Grafos en la Vida Real
Los grafos tienen un sinfín de aplicaciones prácticas en el mundo real, más allá de su utilidad teórica en matemáticas y ciencias de la computación. Se emplean para representar y resolver problemas relacionados con la interconexión, el flujo de información y la optimización de rutas en múltiples industrias y sectores. La versatilidad de los grafos radica en su capacidad para modelar sistemas complejos, permitiendo analizar y gestionar redes de todo tipo.
Desde redes sociales y telecomunicaciones hasta la optimización de rutas de entrega, los grafos se han convertido en una herramienta fundamental en la era digital. Estas estructuras permiten gestionar relaciones entre objetos de manera eficiente, ayudando a solucionar problemas de conectividad, optimización y flujo de datos.
En las siguientes secciones, exploraremos algunos de los ejemplos más importantes y cómo los grafos se utilizan para resolver problemas cotidianos en el ámbito de las redes, la logística y la inteligencia artificial.
Ejemplos reales de aplicaciones de grafos
Los grafos tienen una gran variedad de aplicaciones prácticas en diferentes campos. A continuación, te ofrecemos algunos de los ejemplos más comunes:
- Redes sociales: Las plataformas como Facebook, Instagram y LinkedIn utilizan grafos para modelar las conexiones entre personas. Cada usuario es un vértice, y las relaciones de amistad o seguidores son las aristas.
- Redes de telecomunicaciones: Las compañías telefónicas y de internet usan grafos para representar las conexiones entre dispositivos o estaciones base, optimizando la transmisión de datos y las llamadas entre nodos.
- Sistemas de recomendación: Servicios como Netflix y Spotify utilizan grafos para analizar las relaciones entre usuarios y productos, recomendando contenidos en función de conexiones entre preferencias y patrones de consumo.
- Logística y transporte: Empresas como Amazon o FedEx modelan sus rutas de entrega como grafos, optimizando tiempos y costos mediante algoritmos que buscan las rutas más eficientes.
- Biología computacional: Los grafos son clave en el estudio de redes de proteínas, genes y otros elementos biológicos, ayudando a entender mejor las interacciones en complejas redes biológicas.
Estos ejemplos demuestran cómo los grafos pueden simplificar y mejorar la eficiencia de muchos sistemas en la vida cotidiana. Su capacidad para modelar y gestionar grandes volúmenes de datos hace que sean ideales para resolver problemas que implican múltiples conexiones o relaciones.
¿Cómo se utilizan los grafos en la búsqueda de rutas óptimas?
Uno de los usos más comunes de los grafos es la búsqueda de rutas óptimas, un problema que se presenta en diversas industrias, como la logística, los sistemas de navegación y las redes de telecomunicaciones. Al representar un sistema de rutas como un grafo, donde los nodos son ubicaciones y las aristas representan caminos con un costo o distancia asociado, es posible calcular la ruta más corta o la ruta más eficiente entre dos puntos.
Este tipo de problemas es clave en aplicaciones como los sistemas GPS, donde el objetivo es encontrar la mejor ruta entre dos ubicaciones, minimizando el tiempo de viaje o la distancia recorrida. También es crucial en el diseño de redes de transporte público, donde se busca optimizar las conexiones entre estaciones para mejorar el flujo de pasajeros.
- En transporte: Las compañías de transporte utilizan grafos para encontrar las rutas más cortas o rápidas, minimizando los costos y tiempos de viaje.
- En logística: Empresas de envíos como UPS o DHL utilizan grafos para optimizar la entrega de paquetes, garantizando que los productos lleguen a sus destinos en el menor tiempo posible.
- En redes de telecomunicaciones: Los grafos se utilizan para optimizar el flujo de datos en redes, evitando cuellos de botella y asegurando la entrega rápida y eficiente de información.
Para resolver estos problemas de optimización de rutas, se emplean algoritmos especializados que permiten encontrar la mejor solución de manera eficiente. Algunos de los más conocidos incluyen el algoritmo de Dijkstra y el algoritmo A*, los cuales veremos en detalle a continuación.
Algoritmos en aplicaciones de búsqueda de rutas como Dijkstra y A*
Los algoritmos de búsqueda de rutas son esenciales para resolver problemas relacionados con la optimización en grafos. Entre los más destacados se encuentran el algoritmo de Dijkstra y el algoritmo A*, ambos ampliamente utilizados en sistemas de navegación y planificación de rutas.
El algoritmo de Dijkstra es uno de los más populares para encontrar la ruta más corta entre un nodo de origen y todos los demás nodos en un grafo con aristas de peso no negativo. Es un algoritmo de búsqueda greedy, lo que significa que elige siempre la opción más prometedora en cada paso, garantizando una solución óptima.
Por otro lado, el algoritmo A* es una mejora del algoritmo de Dijkstra que emplea una heurística para priorizar ciertos caminos en función de una estimación del costo total desde el nodo actual hasta el destino. Esto lo hace más eficiente, especialmente en grandes grafos donde hay muchas rutas posibles.
Para ilustrar las similitudes y diferencias entre ambos algoritmos, utilizamos la siguiente tabla comparativa:
| Algoritmo | Principio de búsqueda | Ventajas | Desventajas |
|---|---|---|---|
| Dijkstra | Explora todos los caminos posibles sin priorizar el destino final | Garantiza la ruta más corta en grafos con pesos no negativos | Puede ser lento en grafos grandes |
| A* | Utiliza una heurística para priorizar los caminos más prometedores | Más eficiente en grafos grandes, especialmente cuando la heurística es precisa | Requiere una buena heurística para ser eficaz |
El algoritmo de Dijkstra es ideal para encontrar rutas óptimas en grafos más pequeños o en aquellos donde no se necesita una gran optimización, mientras que el algoritmo A* es preferido en aplicaciones donde la rapidez y la eficiencia son cruciales, como en la búsqueda de rutas en tiempo real en sistemas de navegación.
Ambos algoritmos son fundamentales para aplicaciones de búsqueda de rutas, y su uso depende de las necesidades y características específicas del sistema que se esté modelando.
Representación de los Grafos
Los grafos son una estructura matemática y computacional que se utilizan ampliamente para modelar relaciones y conexiones entre elementos. En términos simples, un grafo está compuesto por nodos (también llamados vértices) y aristas, que representan las conexiones entre dichos nodos.
Para trabajar de manera eficiente con grafos en la programación y en la ciencia de los datos, es esencial conocer las diferentes formas en que se pueden representar. Las representaciones más comunes son las listas de adyacencia y las matrices de adyacencia, cada una con sus propias ventajas y desventajas.
¿Cómo se representan los grafos en estructuras de datos como listas de adyacencia o matrices de adyacencia?
La forma en que se representa un grafo puede tener un gran impacto en la eficiencia y el rendimiento de los algoritmos que se implementan para manipularlo. A continuación, se describen las dos principales representaciones de grafos:
1. Listas de adyacencia:
- Las listas de adyacencia consisten en una lista donde cada nodo tiene una sublista que contiene todos los nodos a los que está conectado por una arista.
- Por ejemplo, si el nodo A está conectado a B y C, en la lista de A se almacenarán B y C.
- Se pueden implementar con vectores o listas enlazadas, dependiendo de las necesidades específicas de almacenamiento y acceso.
2. Matrices de adyacencia:
- Una matriz de adyacencia es una estructura bidimensional que utiliza una matriz cuadrada de tamaño n x n (siendo n el número de nodos) donde cada celda representa si existe o no una arista entre dos nodos.
- Si hay una conexión entre el nodo i y el nodo j, entonces el valor de la posición (i,j) de la matriz será 1 (o algún valor ponderado en caso de grafos ponderados). Si no hay conexión, será 0.
Ventajas y desventajas de las listas de adyacencia frente a las matrices de adyacencia
Ambas representaciones tienen sus pros y contras, dependiendo del tipo de grafos con los que se trabaje y los algoritmos que se necesiten implementar. A continuación, se presentan las ventajas y desventajas de cada una:
Ventajas de las listas de adyacencia:
- Espacio eficiente: Utilizan menos memoria, ya que sólo almacenan las conexiones presentes en el grafo. Para grafos dispersos (donde hay pocas aristas), esta representación es más eficiente.
- Fácil iteración: Facilitan la iteración sobre los nodos adyacentes a un nodo específico, lo que resulta útil en ciertos algoritmos como el recorrido en anchura de un grafo o el recorrido en profundidad.
Desventajas de las listas de adyacencia:
- Verificación de aristas lenta: Comprobar si existe una arista entre dos nodos específicos puede ser costoso, ya que implica recorrer la lista de adyacencia.
- Operaciones costosas: Algunas operaciones, como calcular el número de aristas o determinar si dos nodos están conectados, pueden ser menos eficientes en comparación con las matrices de adyacencia.
Ventajas de las matrices de adyacencia:
- Acceso rápido: Comprobar si existe una arista entre dos nodos es extremadamente rápido (en tiempo constante O(1)) al consultar la matriz.
- Fácil implementación: Las matrices de adyacencia son conceptualmente más simples de implementar y comprender.
Desventajas de las matrices de adyacencia:
- Espacio ineficiente: Para grafos dispersos, ocupan mucho espacio, ya que siempre almacenan n^2 elementos, incluso cuando muchas celdas son 0.
- Iteración costosa: Iterar sobre los nodos adyacentes a un nodo puede ser menos eficiente, ya que se debe recorrer toda una fila de la matriz, incluso si sólo hay unas pocas conexiones.
Comparativa entre listas y matrices de adyacencia:
| Característica | Lista de adyacencia | Matriz de adyacencia |
|---|---|---|
| Uso de espacio | Eficiente para grafos dispersos | Siempre ocupa n^2 espacio |
| Verificación de aristas | Lenta (O(n)) | Rápida (O(1)) |
| Iteración sobre adyacentes | Eficiente | Menos eficiente |
¿Cómo se adapta un algoritmo de recorrido a un grafo dinámico (que cambia con el tiempo)?
En algunos escenarios, los grafos no son estáticos y pueden cambiar con el tiempo. Estos cambios pueden incluir la adición o eliminación de nodos o aristas, lo que introduce nuevos retos en la implementación de algoritmos de recorrido, como el recorrido en anchura (BFS) o el recorrido en profundidad de un grafo (DFS).
Para manejar un grafo dinámico, los algoritmos deben ser capaces de adaptarse a las modificaciones en la estructura del grafo. Algunas de las estrategias utilizadas incluyen:
- Actualizar la estructura de datos: Cada vez que se modifica el grafo, es necesario actualizar la estructura de datos que lo representa, ya sea una lista de adyacencia o una matriz de adyacencia. En el caso de las listas de adyacencia, agregar o eliminar un nodo o una arista es relativamente sencillo, mientras que en las matrices de adyacencia puede implicar reconstruir partes significativas de la matriz.
- Recálculo parcial: Si un algoritmo de recorrido ya ha sido ejecutado en una porción del grafo y el grafo cambia, se puede aplicar una técnica de recálculo parcial en lugar de recalcular todo el recorrido desde cero. Esto es especialmente útil si sólo cambian unas pocas aristas o nodos.
- Algoritmos de recorridos incrementales: Existen algoritmos diseñados específicamente para trabajar con grafos dinámicos. Estos algoritmos permiten agregar o eliminar aristas y nodos sin tener que volver a recorrer todo el grafo.
Los algoritmos de recorrido en grafos dinámicos requieren estrategias adicionales para mantener la coherencia y eficiencia a medida que el grafo cambia. La clave es garantizar que las operaciones de actualización sean rápidas y no afecten significativamente el rendimiento general del recorrido.
Tipos de Recorridos en Grafos
Los recorridos de grafos son fundamentales para trabajar con estructuras de grafos. Permiten explorar y analizar las conexiones entre nodos, resolver problemas de búsqueda, encontrar rutas óptimas, detectar ciclos y mucho más.
Los tipos de recorrido pueden variar según la estrategia utilizada para moverse entre los nodos del grafo.
A continuación, exploraremos qué es un recorrido de grafo, las diferencias entre recorridos completos y parciales, y los dos tipos más comunes: recorrido en anchura y profundidad de un grafo
¿Qué es un recorrido de grafo?
Un recorrido de grafo es el proceso de visitar y explorar los nodos de un grafo siguiendo las aristas que los conectan. Dependiendo de la estrategia de recorrido, los nodos se pueden visitar en un orden particular, lo que permite realizar tareas como:
- Encontrar rutas entre nodos.
- Detectar componentes conectados dentro del grafo.
- Identificar ciclos o caminos más cortos.
Al recorrer un grafo, se pueden visitar algunos o todos los nodos, dependiendo de los objetivos del algoritmo que se esté implementando. Los recorridos son esenciales para la mayoría de los algoritmos que manipulan o analizan grafos dirigidos o no dirigidos.
Durante el recorrido, se mantiene un registro de los nodos que ya han sido visitados para evitar bucles infinitos o visitas repetidas a nodos. Este registro es crucial, especialmente en grafos cíclicos, donde un nodo puede estar conectado indirectamente a sí mismo a través de otros nodos.
Recorridos completos y recorridos parciales
En un recorrido completo, el objetivo es visitar todos los nodos del grafo, asegurando que no quede ningún nodo sin explorar. Este tipo de recorrido es útil cuando se necesita analizar la estructura completa del grafo, como al buscar ciclos o componentes conectados.
Por otro lado, un recorrido parcial implica visitar solo una parte del grafo. Esto puede ser suficiente si estamos buscando un nodo en particular o si nos interesa solo un subconjunto de nodos conectados. Los recorridos parciales son más rápidos, ya que no requieren explorar todo el grafo.
La diferencia clave entre estos tipos de recorridos es el alcance de la exploración:
| Tipo de recorrido | Descripción | Usos comunes |
|---|---|---|
| Recorrido completo | Visita todos los nodos del grafo | Identificar componentes conectados, encontrar ciclos |
| Recorrido parcial | Visita solo una parte del grafo | Buscar un nodo específico, encontrar rutas cortas |
¿Cuáles son los tipos más comunes de recorridos de grafos?
Existen varios métodos para recorrer grafos, pero los dos más utilizados y conocidos son el recorrido recorrido por anchura (BFS por sus siglas en inglés) y el recorrido en profundidad (DFS). Estos métodos ofrecen distintas estrategias de exploración y son adecuados para diferentes tipos de problemas.
Recorrido en anchura (BFS)
El recorrido de anchura de un grafo (BFS, por sus siglas en inglés) explora un grafo comenzando por un nodo inicial y visitando todos los nodos vecinos antes de pasar a los nodos de niveles más profundos. Esto significa que el BFS se mueve nivel por nivel en el grafo, primero recorriendo los nodos más cercanos al nodo de partida y luego avanzando gradualmente hacia nodos más lejanos.
- Para implementar BFS, se utiliza una estructura de datos de cola (FIFO), donde los nodos se insertan a medida que se descubren y se procesan en el orden en que fueron descubiertos.
- Este tipo de recorrido es muy útil para encontrar el camino más corto entre dos nodos en un grafo no ponderado, ya que garantiza que el primer camino encontrado será el más corto en términos de número de aristas.
- Además, BFS puede detectar componentes conectados en un grafo no dirigido.
El algoritmo sigue los siguientes pasos:
- Colocar el nodo inicial en la cola.
- Extraer un nodo de la cola, marcarlo como visitado, y agregar a la cola todos sus vecinos no visitados.
- Repetir el proceso hasta que todos los nodos hayan sido visitados o se haya alcanzado el nodo objetivo.
BFS es útil cuando se necesita explorar nivel a nivel y encontrar el camino más corto en grafos no ponderados. Su implementación es directa y eficiente en estos casos.
Recorrido en profundidad (DFS)
El recorrido primero en profundidad (DFS, por sus siglas en inglés) se adentra lo más posible en un grafo antes de retroceder y explorar otros caminos. Esto significa que DFS explora primero un camino completo desde un nodo inicial hasta un nodo final o hasta que no haya más nodos que explorar, y luego retrocede para explorar otros caminos no visitados.
- DFS se implementa generalmente utilizando una pila (puede ser una pila explícita o la pila del sistema mediante llamadas recursivas) para gestionar los nodos a explorar.
- El DFS es útil cuando queremos explorar completamente un camino antes de probar otros, como al buscar todas las soluciones a un problema, o cuando se necesita explorar a gran profundidad antes que a lo ancho.
- DFS también se utiliza para detectar ciclos en un grafo y para generar árboles de expansión.
Los pasos del algoritmo DFS son los siguientes:
- Comenzar en un nodo inicial y marcarlo como visitado.
- Avanzar a un nodo adyacente no visitado, marcarlo como visitado y repetir el proceso.
- Si no quedan nodos adyacentes por visitar, retroceder y explorar otros caminos no explorados.
- Continuar el proceso hasta que todos los nodos posibles hayan sido visitados.
El DFS es una opción excelente cuando se requiere explorar caminos profundos antes que otros, o cuando se necesitan buscar soluciones exhaustivas en problemas de búsqueda de profundidad.
Tanto el BFS como el DFS son poderosas técnicas de recorrido de grafos, cada una con sus propios casos de uso y ventajas. Mientras que BFS es ideal para problemas de caminos más cortos, DFS sobresale en exploraciones más profundas y en la detección de ciclos dentro de los grafos.
Recorrido en Anchura (BFS)
El Recorrido en Anchura, conocido como Breadth-First Search (BFS), es un algoritmo utilizado en estructuras de datos, específicamente en grafos y árboles. Este algoritmo explora un grafo o árbol nivel por nivel, priorizando los nodos más cercanos al nodo de inicio. El BFS es una técnica crucial en informática, ya que tiene diversas aplicaciones, desde la búsqueda de caminos más cortos hasta la detección de ciclos en grafos.
El BFS es particularmente útil cuando se desea visitar todos los nodos de un grafo, asegurando que se explore cada nodo antes de pasar a niveles más profundos. Su naturaleza garantiza que se siga un orden específico, haciendo que el BFS sea preferido cuando es necesario obtener la solución más cercana o mínima.
Definición y funcionamiento del BFS
El BFS es un algoritmo bfs python de búsqueda en grafos que explora todos los nodos de un grafo o árbol desde un nodo inicial en orden de niveles, es decir, explora primero todos los vecinos directos antes de pasar a los vecinos de los vecinos. Esto lo convierte en un algoritmo no recursivo que se basa en una estructura de datos clave: la cola.
- El BFS comienza en un nodo de inicio.
- Explora todos los nodos adyacentes al nodo inicial.
- Una vez explorados todos los vecinos del primer nodo, pasa a los vecinos de estos.
- Este proceso continúa hasta que se hayan explorado todos los nodos accesibles.
El recorrido en anchura es especialmente útil cuando se quiere garantizar que se visiten primero los nodos más cercanos al nodo de origen, en lugar de profundizar en las ramas del grafo, como ocurre en el Recorrido en Profundidad (DFS).
¿Cómo se implementa BFS utilizando colas?
El BFS se implementa de manera eficiente utilizando una cola. Este tipo de estructura de datos es esencial para mantener el orden de los nodos que se van explorando. A continuación, se describe el proceso:
- Se comienza con un nodo inicial que se agrega a la cola.
- Se marca el nodo como visitado para evitar volver a explorarlo.
- Se extrae el primer nodo de la cola y se exploran todos sus vecinos.
- Los vecinos no visitados se agregan a la cola para ser procesados más tarde.
- El proceso continúa hasta que la cola esté vacía, lo que indica que se han explorado todos los nodos accesibles.
La clave de la implementación es que, al utilizar una cola, el BFS siempre asegura que los nodos se exploren en el orden correcto, respetando el principio de "primero en entrar, primero en salir" (FIFO).
Ejemplo de recorrido en anchura
Para ilustrar mejor el funcionamiento del BFS, consideremos un ejemplo simple de un grafo no ponderado:
| Nodo | Vecinos |
|---|---|
| A | B, C |
| B | D, E |
| C | F |
| D | |
| E | |
| F |
Si aplicamos el BFS empezando en el nodo A, el recorrido sería el siguiente:
- Se inicia en A y se agregan los vecinos B y C a la cola.
- Se extrae B de la cola y se agregan sus vecinos D y E a la cola.
- Se extrae C de la cola y se agrega su vecino F a la cola.
- El siguiente en la cola es D, pero no tiene vecinos, por lo que se extrae sin agregar más nodos.
- Se extraen E y F, completando el recorrido.
Este ejemplo muestra cómo el BFS visita todos los nodos en niveles, asegurando que los nodos más cercanos al nodo inicial se exploren primero.
¿Cómo ayuda el BFS en la búsqueda de caminos más cortos?
Una de las principales ventajas del BFS es su capacidad para encontrar caminos más cortos en grafos no ponderados. Esto se debe a su naturaleza de explorar primero todos los nodos cercanos antes de pasar a nodos más distantes.
Cuando se utiliza BFS para buscar un camino entre dos nodos, el algoritmo garantiza que el primer camino encontrado será el más corto en términos de número de aristas (o conexiones). Esto lo hace ideal para aplicaciones en las que se necesita una solución rápida sin considerar el peso o costo de las aristas.
- El BFS garantiza el camino más corto en grafos no ponderados porque explora todos los vecinos antes de profundizar en el grafo.
- Funciona mejor cuando las distancias entre los nodos son iguales, es decir, no se consideran pesos en las conexiones.
- Es útil para problemas de rutas mínimas en redes como redes sociales, mapas y otros sistemas de grafos.
Es importante destacar que en grafos ponderados, el BFS no garantiza el camino más corto, ya que no toma en cuenta los pesos de las aristas. Para estos casos, se suelen emplear otros algoritmos como Dijkstra.
¿Cómo se puede utilizar BFS para encontrar la distancia mínima entre dos nodos en un grafo no ponderado?
El BFS es ideal para encontrar la distancia mínima entre dos nodos en un grafo no ponderado. Dado que explora los nodos por niveles, cada nivel adicional representa una unidad más en la distancia.
- Se comienza en el nodo de origen y se establece la distancia como 0.
- Se exploran todos los nodos adyacentes, asignando una distancia de 1 a esos nodos.
- Para cada nodo siguiente, se incrementa la distancia en 1 a medida que se exploran nuevos niveles.
- El proceso continúa hasta llegar al nodo de destino.
Una vez que el algoritmo alcanza el nodo objetivo, la distancia registrada será la mínima cantidad de aristas que separan a los dos nodos. De esta manera, el BFS se convierte en una técnica clave para problemas de rutas cortas en grafos sin pesos.
Recorrido en Profundidad (DFS)
Definición y funcionamiento del DFS
El Recorrido en Profundidad, comúnmente conocido como DFS por sus siglas en inglés (Depth-First Search), es un algoritmo de búsqueda utilizado en estructuras de datos como grafos y árboles. El DFS se adentra en un grafo lo más lejos posible antes de retroceder y explorar otros caminos. Este enfoque se asemeja a un proceso de exploración en el que se sigue un camino hasta que no es posible avanzar más, luego se retrocede para explorar otras rutas alternativas.
El funcionamiento del DFS se basa en la exploración de vértices adyacentes, moviéndose hacia uno de ellos y marcándolo como visitado. Este proceso se repite hasta que se exploran todos los caminos posibles desde el vértice inicial. La naturaleza recursiva de DFS permite que se realice un seguimiento de los nodos visitados y no visitados de manera eficiente.
DFS es útil cuando se desea encontrar todas las soluciones posibles en problemas de búsqueda, explorar todas las ramas de un árbol o identificar componentes fuertemente conectados en un grafo. Se usa en una amplia variedad de aplicaciones, desde juegos hasta la resolución de problemas complejos en inteligencia artificial.
- Explora el grafo siguiendo un camino hasta llegar al final.
- Retrocede una vez que no puede avanzar más.
- Utiliza una estructura de datos como pila para almacenar los nodos pendientes por explorar.
¿Cómo se implementa DFS utilizando pilas (o recursión)?
El DFS puede implementarse de dos formas principales: utilizando recursión o una pila. La versión recursiva es más común, ya que el propio sistema de llamadas recursivas actúa como una pila, pero también se puede implementar explícitamente utilizando una pila manual.
Cuando se usa recursión, cada llamada a la función representa una nueva exploración de un nodo, donde se marcan los nodos como visitados y se realiza la llamada recursiva a los vecinos no visitados. El proceso continúa hasta que no quedan vecinos no explorados, momento en el que la recursión retrocede al nodo anterior.
En cambio, en la implementación iterativa utilizando una pila:
- Se inicializa una pila vacía y se empuja el nodo inicial.
- Mientras la pila no esté vacía, se extrae el nodo de la cima y se verifica si ha sido visitado.
- Si no ha sido visitado, se marca como visitado y se empujan sus vecinos no visitados a la pila.
Ambos métodos son funcionalmente equivalentes, aunque la implementación recursiva tiende a ser más elegante y comprensible en muchos contextos.
Ejemplo de recorrido en profundidad
Veamos un ejemplo sencillo de cómo funciona el DFS en un grafo. Imaginemos un grafo con los siguientes nodos y aristas:
- Nodos: A, B, C, D, E
- Aristas: A-B, A-C, B-D, C-E
Si comenzamos el DFS en el nodo A, el algoritmo seguirá este recorrido:
- Se comienza en A y se marca como visitado.
- Se mueve al siguiente nodo adyacente no visitado, en este caso B, y se marca como visitado.
- Desde B, el algoritmo se mueve a D, marcándolo como visitado.
- Como D no tiene más nodos adyacentes no visitados, el algoritmo retrocede a B y luego a A.
- Desde A, el DFS ahora explora C, luego continúa hasta E.
El orden de visita de los nodos sería: A → B → D → C → E.
¿Cómo se utiliza DFS en la detección de ciclos dentro de un grafo?
Una de las aplicaciones más importantes del DFS es la detección de ciclos en un grafo. Un ciclo ocurre cuando existe un camino que comienza y termina en el mismo nodo, formando un bucle. La detección de estos ciclos es crucial en muchas aplicaciones, como la verificación de dependencias en sistemas de software o la planificación de recursos.
En un grafo dirigido, para detectar ciclos utilizando DFS:
- Se comienza un recorrido DFS desde cualquier nodo, marcándolo como visitado.
- Si se llega a un nodo que ya está en el camino actual del DFS (es decir, ha sido visitado pero aún no se ha terminado de procesar), entonces se ha encontrado un ciclo.
- Si el nodo ya ha sido visitado pero no está en el camino actual, no hay ciclo en esa rama.
Este enfoque es eficiente y permite detectar ciclos en tiempo lineal, lo que lo hace ideal para problemas que involucren la búsqueda de dependencias cíclicas en grandes grafos.
¿Cómo se aplica DFS en la planificación de tareas (ordenación topológica)?
La ordenación topológica es una técnica para organizar las tareas de manera que se respeten las dependencias entre ellas. En términos de un grafo, si hay una arista de un nodo A a un nodo B, significa que la tarea A debe completarse antes que la tarea B. El DFS es una herramienta fundamental para calcular esta ordenación.
El proceso para aplicar DFS en la ordenación topológica es el siguiente:
- Realizar un recorrido DFS desde cualquier nodo del grafo.
- Una vez que se termina de explorar completamente un nodo (es decir, no tiene vecinos no visitados), se agrega a una lista o pila que representa el orden de ejecución de las tareas.
- El resultado final será la lista en orden inverso, donde las primeras tareas a realizar están al final de la pila o lista.
Este enfoque garantiza que todas las dependencias se respeten, y es una técnica común en sistemas de compilación, planificación de proyectos y gestión de flujos de trabajo. Además, es especialmente útil cuando se necesita ejecutar tareas que tienen dependencias complejas, como la construcción de software o la organización de procesos en sistemas distribuidos.
El DFS es un algoritmo versátil con múltiples aplicaciones, desde la detección de ciclos hasta la planificación de tareas, lo que lo convierte en una herramienta indispensable en la informática moderna.
Comparación entre BFS y DFS
Los algoritmos de búsqueda en grafos son una parte fundamental de las ciencias de la computación, y dos de los más utilizados son BFS (Breadth-First Search) y DFS (Depth-First Search). Ambos métodos son esenciales para la navegación y exploración de grafos y árboles, pero abordan el problema de forma distinta, lo que les otorga ventajas y desventajas en diferentes situaciones.
¿Cuáles son las diferencias entre BFS y DFS en términos de algoritmo?
La principal diferencia entre BFS y DFS radica en el orden en que exploran los vértices del grafo. Mientras que BFS explora los vértices nivel por nivel, comenzando desde el nodo inicial y extendiéndose hacia los nodos más cercanos, DFS sigue un camino profundo en el grafo, explorando tan lejos como sea posible antes de retroceder.
- BFS utiliza una cola (FIFO, First In First Out) para gestionar los vértices por explorar. Esto asegura que se exploren primero los vértices más cercanos al nodo inicial.
- DFS, por otro lado, utiliza una pila (LIFO, Last In First Out), lo que le permite profundizar en un camino hasta llegar a un nodo sin más vértices no explorados, y solo entonces retrocede.
En términos de funcionamiento, BFS es más adecuado para encontrar el camino más corto en grafos no ponderados, mientras que DFS es más eficiente para detectar ciclos o explorar todas las posibles rutas desde un nodo.
Otra diferencia clave es cómo cada algoritmo se estructura:
| Aspecto | BFS | DFS |
|---|---|---|
| Estructura | Cola (FIFO) | Pila (LIFO) |
| Exploración | Nivel por nivel | Profundidad hasta el final |
| Ideal para | Encontrar caminos más cortos | Detectar ciclos y explorar todas las rutas |
¿Qué es la complejidad computacional de BFS y DFS?
Ambos algoritmos tienen una complejidad computacional muy similar en términos de tiempo. La complejidad de BFS y DFS depende de la cantidad de nodos (V) y aristas (E) en el grafo, siendo:
- La complejidad de BFS es O(V + E), ya que explora cada nodo y cada arista exactamente una vez.
- La complejidad de DFS también es O(V + E) por la misma razón: cada nodo y arista se recorre una vez.
En cuanto a la complejidad espacial, existe una diferencia notable:
- BFS utiliza más memoria, ya que debe almacenar todos los nodos de un nivel antes de proceder al siguiente. Su complejidad espacial es O(V) en el peor caso.
- DFS es más eficiente en espacio, ya que solo necesita almacenar los nodos del camino actual y sus ancestros. Su complejidad espacial es O(V) en el peor caso si el grafo es un árbol, pero podría ser menor dependiendo del recorrido.
¿Cuándo es más eficiente usar BFS frente a DFS?
La eficiencia de BFS frente a DFS depende del problema que se esté resolviendo:
- BFS es más eficiente cuando se necesita encontrar el camino más corto en un grafo no ponderado, ya que explora todos los vértices de un nivel antes de pasar al siguiente, garantizando que se encuentre el camino más corto desde el nodo inicial a cualquier otro nodo.
- DFS es preferible cuando se quiere explorar completamente un grafo o cuando se busca un camino en profundidad, como en problemas donde es necesario recorrer todas las rutas posibles, por ejemplo, en la generación de laberintos o en algoritmos que requieren el análisis de caminos profundos.
En general, usa BFS cuando el problema requiere encontrar soluciones cercanas o cuando el grafo es ancho y poco profundo. Usa DFS cuando el grafo tiene una estructura más profunda o cuando la solución probablemente se encuentre en las profundidades del grafo, de esta forma podremos ver en ancho y profundidad la selección según la necesidad.
¿Cómo afectan los ciclos en los grafos a los recorridos BFS y DFS?
La presencia de ciclos en un grafo puede afectar tanto a BFS como a DFS si no se toman las medidas adecuadas para evitarlos. Los ciclos podrían llevar a que los algoritmos exploren los mismos nodos más de una vez, lo que causaría un bucle infinito.
- En BFS, los ciclos se manejan fácilmente marcando los nodos visitados. Una vez que un nodo ha sido explorado, no se vuelve a visitar, lo que evita el bucle.
- En DFS, también es necesario marcar los nodos visitados, pero la estructura recursiva del algoritmo podría llevar a problemas de desbordamiento de pila en grafos con ciclos grandes si no se maneja correctamente.
Los ciclos en un grafo requieren que ambos algoritmos implementen una forma de seguimiento de nodos visitados. De lo contrario, podrían caer en recursiones infinitas o búsquedas ineficientes.
Implementación de Recorridos en Lenguajes de Programación
Recorridos en Grafos con Python
Los grafos son una estructura de datos fundamental en la informática, utilizada para modelar relaciones entre entidades. Python, con su sintaxis clara y amplia biblioteca estándar, se ha convertido en uno de los lenguajes más populares para implementar algoritmos de recorridos en grafos, como BFS (Breadth-First Search) y DFS (Depth-First Search). A continuación, exploramos las ventajas de usar Python, implementaciones básicas de estos algoritmos y el uso de herramientas avanzadas como NetworkX.
Ventajas de usar Python para trabajar con grafos
Python es ampliamente reconocido por su facilidad de uso y versatilidad, lo que lo convierte en una elección ideal para implementar y trabajar con grafos. Algunas de las principales ventajas de usar Python incluyen:
- Sintaxis simple y legible: Python permite escribir código claro, lo que facilita la comprensión de algoritmos complejos.
- Soporte extenso de bibliotecas: Python cuenta con bibliotecas especializadas como NetworkX, igraph y Graph-tool, diseñadas para simplificar el trabajo con grafos.
- Comunidad activa: La comunidad de Python proporciona documentación, tutoriales y soluciones prácticas que facilitan la resolución de problemas.
- Integración con herramientas científicas: Librerías como NumPy y Matplotlib permiten realizar análisis avanzados y visualizaciones efectivas de grafos.
Estas ventajas hacen de Python una herramienta poderosa para investigadores, desarrolladores y académicos que trabajan con estructuras de grafos.
Implementación básica del BFS y DFS
Los algoritmos de BFS y DFS son dos de los métodos más comunes para explorar grafos. Ambos tienen aplicaciones en áreas como la búsqueda en redes, la resolución de problemas y la optimización.
Breadth-First Search (BFS)
El BFS es un algoritmo de búsqueda por niveles que explora los nodos de un grafo en capas, comenzando desde un nodo inicial y visitando primero todos los vecinos inmediatos antes de pasar a los vecinos de nivel siguiente. Aquí está su implementación básica en Python:
from collections import deque
def bfs(graph, start):
visited = set()
queue = deque([start])
while queue:
node = queue.popleft()
if node not in visited:
print(node, end=" ")
visited.add(node)
queue.extend(graph[node] - visited)
# Ejemplo de grafo representado como un diccionario
grafo = {
'A': {'B', 'C'},
'B': {'A', 'D', 'E'},
'C': {'A', 'F'},
'D': {'B'},
'E': {'B', 'F'},
'F': {'C', 'E'}
}
bfs(grafo, 'A')
En este código, el grafo está representado como un diccionario de conjuntos, donde las claves son nodos y los valores son conjuntos de nodos adyacentes.
Depth-First Search (DFS)
El DFS, en contraste, utiliza un enfoque recursivo o basado en pilas para explorar los nodos más profundamente antes de retroceder. Su implementación básica es la siguiente:
def dfs(graph, node, visited=None):
if visited is None:
visited = set()
if node not in visited:
print(node, end=" ")
visited.add(node)
for neighbor in graph[node]:
dfs(graph, neighbor, visited)
# Uso del mismo grafo
dfs(grafo, 'A')
Este algoritmo es útil para problemas que requieren explorar todas las posibles rutas en un grafo.
Uso de bibliotecas populares como NetworkX
NetworkX es una biblioteca poderosa y ampliamente utilizada para trabajar con grafos en Python. Proporciona herramientas fáciles de usar para crear, analizar y visualizar grafos complejos. A continuación, se describe cómo emplear NetworkX para realizar recorridos BFS y DFS.
Creación y recorrido de grafos con NetworkX
Con NetworkX, la creación de un grafo es sencilla. Los métodos para realizar BFS y DFS están integrados en la biblioteca:
import networkx as nx
# Crear un grafo dirigido
G = nx.DiGraph()
G.add_edges_from([
('A', 'B'), ('A', 'C'), ('B', 'D'), ('B', 'E'),
('C', 'F'), ('E', 'F')
])
# BFS usando NetworkX
print("BFS:", list(nx.bfs_edges(G, 'A')))
# DFS usando NetworkX
print("DFS:", list(nx.dfs_edges(G, 'A')))
NetworkX maneja automáticamente la estructura y los algoritmos del grafo, lo que simplifica la implementación y reduce los errores.
Visualización de grafos
Además de los algoritmos de recorrido, NetworkX incluye herramientas para la visualización de grafos, lo que facilita su comprensión. A continuación, se muestra cómo visualizar un grafo:
import matplotlib.pyplot as plt
nx.draw(G, with_labels=True, node_color='lightblue', edge_color='gray')
plt.show()
El resultado es una representación gráfica clara que ilustra las relaciones entre los nodos.
Comparación de BFS y DFS
Los algoritmos BFS y DFS tienen diferencias clave que los hacen adecuados para distintos casos de uso. A continuación, se presenta una tabla comparativa:
| Característica | BFS | DFS |
|---|---|---|
| Orden de exploración | Nivel por nivel | Profundidad primero |
| Uso de memoria | Mayor (cola) | Menor (pila o recursión) |
| Aplicaciones | Búsqueda de rutas más cortas | Detección de ciclos |
Ambos algoritmos tienen sus méritos, y la elección entre ellos depende del problema específico que se está resolviendo.
Recorridos en Grafos con Java
Estructuras de datos utilizadas en Java
En Java, las estructuras de datos son esenciales para la implementación de algoritmos de grafos como BFS y DFS. Gracias a la biblioteca estándar de Java y su flexibilidad, es posible usar estructuras como ArrayList y LinkedList para representar y manipular grafos de manera eficiente. Estas estructuras son particularmente útiles para implementar listas de adyacencia, una de las formas más comunes de representar grafos.
ArrayList
ArrayList es una implementación dinámica de una lista en Java, que permite almacenar elementos en un arreglo redimensionable. Para los grafos, ArrayList se utiliza para almacenar las listas de adyacencia de cada nodo:
- Ventajas: Acceso rápido a los elementos mediante índices.
- Desventajas: Operaciones de inserción y eliminación más lentas en comparación con otras estructuras como LinkedList.
import java.util.ArrayList;
public class Grafo {
private ArrayList<ArrayList> adjList;
public Grafo(int vertices) {
adjList = new ArrayList<>();
for (int i = 0; i < vertices; i++) {
adjList.add(new ArrayList<>());
}
}
public void addEdge(int src, int dest) {
adjList.get(src).add(dest);
}
}
LinkedList
LinkedList es otra estructura ampliamente utilizada para representar grafos en Java. Es ideal para casos donde las operaciones de inserción y eliminación son frecuentes.
- Ventajas: Operaciones rápidas de inserción y eliminación.
- Desventajas: Acceso más lento a los elementos debido a su estructura enlazada.
import java.util.LinkedList;
public class Grafo {
private LinkedList[] adjList;
public Grafo(int vertices) {
adjList = new LinkedList[vertices];
for (int i = 0; i < vertices; i++) {
adjList[i] = new LinkedList<>();
}
}
public void addEdge(int src, int dest) {
adjList[src].add(dest);
}
}
Ambas estructuras, ArrayList y LinkedList, son ampliamente utilizadas dependiendo de los requisitos específicos del problema.
Ejemplos de BFS y DFS
Los algoritmos BFS y DFS son fundamentales para la exploración de grafos. A continuación, se presentan implementaciones detalladas de ambos algoritmos en Java.
Implementación de BFS en Java
El algoritmo Breadth-First Search (BFS) utiliza una cola para explorar los nodos nivel por nivel. Aquí se muestra su implementación básica:
import java.util.*;
public class BFSExample {
private LinkedList[] adjList;
public BFSExample(int vertices) {
adjList = new LinkedList[vertices];
for (int i = 0; i < vertices; i++) {
adjList[i] = new LinkedList<>();
}
}
public void addEdge(int src, int dest) {
adjList[src].add(dest);
}
public void bfs(int start) {
boolean[] visited = new boolean[adjList.length];
Queue queue = new LinkedList<>();
visited[start] = true;
queue.add(start);
while (!queue.isEmpty()) {
int node = queue.poll();
System.out.print(node + " ");
for (int neighbor : adjList[node]) {
if (!visited[neighbor]) {
visited[neighbor] = true;
queue.add(neighbor);
}
}
}
}
public static void main(String[] args) {
BFSExample graph = new BFSExample(6);
graph.addEdge(0, 1);
graph.addEdge(0, 2);
graph.addEdge(1, 3);
graph.addEdge(1, 4);
graph.addEdge(2, 5);
System.out.println("Recorrido BFS:");
graph.bfs(0);
}
}
Este código utiliza una estructura de cola y un arreglo para rastrear los nodos visitados.
Implementación de DFS en Java
El algoritmo Depth-First Search (DFS) utiliza una pila o recursión para explorar nodos en profundidad. Aquí está su implementación:
import java.util.*;
public class DFSExample {
private LinkedList[] adjList;
public DFSExample(int vertices) {
adjList = new LinkedList[vertices];
for (int i = 0; i < vertices; i++) {
adjList[i] = new LinkedList<>();
}
}
public void addEdge(int src, int dest) {
adjList[src].add(dest);
}
public void dfs(int node, boolean[] visited) {
visited[node] = true;
System.out.print(node + " ");
for (int neighbor : adjList[node]) {
if (!visited[neighbor]) {
dfs(neighbor, visited);
}
}
}
public static void main(String[] args) {
DFSExample graph = new DFSExample(6);
graph.addEdge(0, 1);
graph.addEdge(0, 2);
graph.addEdge(1, 3);
graph.addEdge(1, 4);
graph.addEdge(2, 5);
System.out.println("Recorrido DFS:");
graph.dfs(0, new boolean[6]);
}
}
La implementación de DFS utiliza un enfoque recursivo para explorar los nodos y sus vecinos.
Manejo de grafos dirigidos y no dirigidos
En los grafos, las conexiones entre nodos pueden ser dirigidas o no dirigidas. Esto afecta cómo se representan y recorren los grafos.
Grafos dirigidos
En un grafo dirigido, las aristas tienen una dirección, lo que significa que la relación entre nodos es unidireccional.
- Representación: Usar una lista de adyacencia donde las aristas apuntan en una dirección específica.
- Ejemplo: Una red de carreteras con sentido único.
Grafos no dirigidos
En un grafo no dirigido, las aristas no tienen dirección, lo que indica que la relación entre nodos es bidireccional.
- Representación: Cada arista se añade en ambas direcciones en la lista de adyacencia.
- Ejemplo: Una red de amigos en una plataforma social.
A continuación, se muestra cómo manejar grafos dirigidos y no dirigidos:
// Agregar aristas dirigidas
public void addDirectedEdge(int src, int dest) {
adjList[src].add(dest);
}
// Agregar aristas no dirigidas
public void addUndirectedEdge(int src, int dest) {
adjList[src].add(dest);
adjList[dest].add(src);
}
El manejo de grafos dirigidos y no dirigidos depende de la lógica del problema y de cómo se desea explorar las relaciones entre nodos.
Recorridos en Grafos con C++
Uso de vectores y listas de adyacencia en C++
En C++, la representación de grafos se logra de manera eficiente utilizando vectores y listas de adyacencia. Estas estructuras permiten modelar grafos de manera compacta y optimizada, facilitando operaciones como la adición de aristas, la búsqueda y el recorrido de nodos.
Vectores
Los vectores en C++ son contenedores dinámicos que se adaptan bien para representar listas de adyacencia. Cada nodo se asocia con un vector que contiene sus nodos adyacentes. Esto permite un acceso rápido y una representación compacta del grafo.
#include <vector>
#include <iostream>
using namespace std;
class Grafo {
vector<vector> adjList;
public:
Grafo(int vertices) {
adjList.resize(vertices);
}
void agregarArista(int src, int dest) {
adjList[src].push_back(dest);
adjList[dest].push_back(src); // Para grafos no dirigidos
}
void mostrarGrafo() {
for (int i = 0; i < adjList.size(); i++) {
cout << "Nodo " << i << ": ";
for (int vecino : adjList[i]) {
cout << vecino << " ";
}
cout << endl;
}
}
};
int main() {
Grafo grafo(5);
grafo.agregarArista(0, 1);
grafo.agregarArista(0, 4);
grafo.agregarArista(1, 2);
grafo.agregarArista(1, 3);
grafo.mostrarGrafo();
return 0;
}
Listas de adyacencia
Las listas de adyacencia, implementadas con listas enlazadas o vectores de listas, son útiles para grafos dispersos. Estas listas ocupan menos memoria que las matrices de adyacencia y son ideales para problemas con grafos grandes.
#include <list>
class Grafo {
list* adjList;
int vertices;
public:
Grafo(int v) {
vertices = v;
adjList = new list[v];
}
void agregarArista(int src, int dest) {
adjList[src].push_back(dest);
}
void mostrarGrafo() {
for (int i = 0; i < vertices; i++) {
cout << "Nodo " << i << ": ";
for (int vecino : adjList[i]) {
cout << vecino << " ";
}
cout << endl;
}
}
};
Implementaciones eficientes con STL (Standard Template Library)
El uso de la STL en C++ proporciona herramientas altamente optimizadas como queue, stack y priority_queue para realizar recorridos y operaciones en grafos.
BFS usando STL
El algoritmo BFS utiliza una cola para recorrer los nodos nivel por nivel. Aquí está su implementación:
#include <queue>
void bfs(int start, vector<vector>& adjList, vector& visited) {
queue q;
visited[start] = true;
q.push(start);
while (!q.empty()) {
int node = q.front();
q.pop();
cout << node << " ";
for (int neighbor : adjList[node]) {
if (!visited[neighbor]) {
visited[neighbor] = true;
q.push(neighbor);
}
}
}
}
Aplicaciones en problemas competitivos
Los algoritmos de grafos son fundamentales en programación competitiva. Se utilizan para resolver problemas como:
- Detección de ciclos en grafos dirigidos y no dirigidos.
- Algoritmos de rutas más cortas, como Dijkstra y Floyd-Warshall.
- Determinación de componentes conexas en grafos no dirigidos.
Recorridos en Grafos con JavaScript
Representación de grafos en JavaScript
En JavaScript, los grafos suelen representarse utilizando objetos o Map. Esto permite una manipulación sencilla y directa de nodos y aristas, lo cual es ideal para aplicaciones web y sistemas interactivos.
// Representación de un grafo usando un objeto
const grafo = {
0: [1, 2],
1: [0, 3, 4],
2: [0, 5],
3: [1],
4: [1],
5: [2]
};
Aplicaciones de BFS y DFS en desarrollo web
Los algoritmos BFS y DFS se utilizan en JavaScript para buscar rutas, resolver laberintos y optimizar redes.
Implementación de BFS
function bfs(grafo, start) {
const visited = new Set();
const queue = [start];
while (queue.length > 0) {
const node = queue.shift();
if (!visited.has(node)) {
console.log(node);
visited.add(node);
queue.push(...grafo[node].filter(n => !visited.has(n)));
}
}
}
Implementación de DFS
function dfs(grafo, start, visited = new Set()) {
if (visited.has(start)) return;
console.log(start);
visited.add(start);
for (const neighbor of grafo[start]) {
dfs(grafo, neighbor, visited);
}
}
Integración con frameworks para análisis de datos
Frameworks como D3.js y three.js facilitan la visualización y análisis de datos en aplicaciones web que involucran grafos.
- D3.js: Permite crear gráficos interactivos y diagramas de grafos dinámicos.
- three.js: Ideal para representar grafos en 3D y generar visualizaciones inmersivas.
Comparación de Implementaciones entre Lenguajes
Diferencias en la sintaxis y enfoque
Los lenguajes de programación como Python, Java, C++ y JavaScript tienen diferencias significativas en su estructura sintáctica y enfoque hacia la implementación de algoritmos de grafos. Estas diferencias impactan la forma en que los desarrolladores diseñan soluciones y manejan operaciones complejas.
| Lenguaje | Sintaxis | Enfoque |
|---|---|---|
| Python | Sintaxis concisa y legible. | Orientado a bibliotecas como NetworkX para simplificar la implementación. |
| Java | Verbosa con estructuras fuertemente tipadas. | Uso extensivo de clases y objetos para modelar grafos. |
| C++ | Mayor control gracias a la STL y punteros. | Enfoque en eficiencia y optimización de recursos. |
| JavaScript | Sintaxis dinámica y menos estricta. | Práctico para aplicaciones web y visualización de grafos. |
Ventajas y desventajas en la ejecución
Cada lenguaje tiene fortalezas y debilidades en la ejecución de algoritmos de grafos, dependiendo del caso de uso y el contexto en que se utilicen.
- Python:
- Ventajas: Simplicidad y disponibilidad de bibliotecas como NetworkX.
- Desventajas: Menor velocidad en comparación con lenguajes compilados como C++.
- Java:
- Ventajas: Buen balance entre rendimiento y facilidad de uso.
- Desventajas: Sintaxis más compleja que puede ralentizar el desarrollo.
- C++:
- Ventajas: Excelente rendimiento y control de recursos.
- Desventajas: Mayor complejidad en la implementación.
- JavaScript:
- Ventajas: Ideal para aplicaciones web y visualizaciones dinámicas.
- Desventajas: No es el lenguaje más eficiente para operaciones intensivas de grafos.
Escenarios ideales para cada lenguaje
Dependiendo del contexto del proyecto, un lenguaje puede ser más adecuado que otro para implementar algoritmos de grafos.
- Python: Perfecto para investigación y prototipos rápidos gracias a su simplicidad y potentes bibliotecas.
- Java: Ideal para aplicaciones empresariales donde la robustez y la interoperabilidad son clave.
- C++: Elegido en programación competitiva y aplicaciones donde el rendimiento es crítico.
- JavaScript: Excelente para desarrollo web y proyectos que requieren interfaces visuales interactivas.
Herramientas y Librerías para Grafos
NetworkX (Python)
NetworkX es una biblioteca de Python diseñada para trabajar con grafos y redes. Ofrece herramientas para crear, manipular y analizar grafos de forma eficiente.
- Soporte para grafos dirigidos y no dirigidos.
- Funciones para análisis de redes, como detección de comunidades y rutas más cortas.
- Facilidad de uso gracias a su integración con Python.
import networkx as nx
# Crear un grafo
G = nx.Graph()
G.add_edge(1, 2)
G.add_edge(2, 3)
# Visualizar el grafo
print(G.nodes)
print(G.edges)
JGraphT (Java)
JGraphT es una biblioteca de Java ampliamente utilizada para modelar y analizar grafos. Es conocida por su flexibilidad y capacidad para soportar grafos complejos.
- Implementación de algoritmos como Dijkstra y Kruskal.
- Soporte para grafos ponderados y no ponderados.
- Integración con otras herramientas de análisis en Java.
Boost Graph Library (C++)
La Boost Graph Library (BGL) es una colección de herramientas en C++ diseñadas para trabajar con grafos. Es una opción popular en aplicaciones que requieren alto rendimiento.
- Compatible con la STL, lo que permite integración directa en proyectos complejos.
- Optimización para recorridos y análisis de grafos grandes.
- Soporte para algoritmos avanzados como Prim y Bellman-Ford.
Graphology (JavaScript)
Graphology es una biblioteca de JavaScript diseñada para manejar grafos en entornos web. Es ideal para aplicaciones que requieren análisis y visualización en tiempo real.
- Compatible con Node.js y navegadores.
- Soporte para grafos dinámicos y análisis interactivo.
- Integración con frameworks como D3.js para visualización.
// Crear un grafo en Graphology
const {Graph} = require('graphology');
const graph = new Graph();
graph.addNode('A');
graph.addNode('B');
graph.addEdge('A', 'B');
console.log(graph.nodes());
Caminos, Ciclos y Árboles en Grafos
En el mundo de los grafos, los conceptos de caminos, ciclos y árboles son fundamentales para comprender cómo se relacionan los nodos y las aristas. Estos conceptos son utilizados en una amplia variedad de aplicaciones, desde la optimización de rutas hasta la organización de datos. A continuación, se explorarán en detalle los ciclos, árboles de expansión, componentes conexas y las diferencias entre recorridos en árboles y grafos generales.
¿Qué es un ciclo en un grafo y cómo afecta a los recorridos?
Un ciclo en un grafo es un camino que comienza y termina en el mismo nodo, sin repetir aristas ni nodos, excepto el inicial y el final. Los ciclos son un elemento clave en los grafos, y su presencia puede influir significativamente en cómo se realizan los recorridos.
En términos de recorridos, los ciclos pueden complicar los algoritmos de búsqueda, como BFS y DFS, ya que pueden llevar a que los algoritmos visiten repetidamente los mismos nodos, entrando en bucles infinitos. Para evitar esto, ambos algoritmos necesitan implementar un mecanismo para marcar los nodos visitados y evitar revisitar nodos que ya hayan sido procesados.
- En DFS, el ciclo puede hacer que el algoritmo continúe recursivamente visitando nodos ya explorados, lo que podría llevar a un desbordamiento de pila si el ciclo no es gestionado adecuadamente.
- En BFS, el algoritmo podría quedar atrapado en el ciclo, visitando nodos una y otra vez, lo que haría que la búsqueda sea ineficiente.
Por lo tanto, los ciclos en los grafos requieren un manejo cuidadoso, particularmente en los recorridos que exploran caminos entre nodos, como ocurre con BFS y DFS.
¿Qué es un árbol de expansión y cómo se relaciona con los recorridos?
Un árbol de expansión es un subgrafo de un grafo general que incluye todos los nodos del grafo original, pero sin contener ciclos. En otras palabras, es una versión del grafo que conecta todos los nodos con el menor número posible de aristas y sin crear ciclos. Los árboles de expansión se utilizan frecuentemente en problemas de optimización, como la búsqueda de la mínima cantidad de conexiones necesarias para vincular todos los nodos de una red.
Los recorridos BFS y DFS son fundamentales para construir árboles de expansión. Durante el recorrido de un grafo, se puede generar un árbol de expansión seleccionando aristas que no formen ciclos. De hecho, ambos algoritmos pueden producir diferentes tipos de árboles:
- Árbol BFS: El árbol de expansión generado por BFS conecta los nodos siguiendo los niveles del grafo, creando una estructura en la que los nodos del mismo nivel están a la misma distancia del nodo raíz.
- Árbol DFS: El árbol de expansión generado por DFS tiende a profundizar en un camino antes de retroceder, lo que crea una estructura más "profunda" y alargada en comparación con BFS.
Estos árboles de expansión son útiles en algoritmos como Prim o Kruskal, que buscan árboles de expansión mínimos en grafos ponderados, es decir, el árbol que conecta todos los nodos con el costo mínimo en términos de aristas.
¿Cómo se identifican las componentes conexas en un grafo utilizando BFS o DFS?
Una componente conexa en un grafo es un subgrafo en el que cualquier par de nodos está conectado por un camino, y no existe ninguna arista que lo conecte con el resto del grafo. Identificar estas componentes es crucial para entender la estructura del grafo y para realizar análisis posteriores.
Los algoritmos de búsqueda, tanto BFS como DFS, son métodos eficaces para identificar componentes conexas en un grafo. El proceso general es el siguiente:
- Inicialización: Comenzamos con todos los nodos sin marcar. Cada vez que un nodo no marcado es encontrado, se inicia una nueva búsqueda BFS o DFS desde ese nodo.
- Exploración: A medida que avanzamos por el grafo, vamos marcando los nodos visitados, lo que garantiza que no sean explorados de nuevo. Todos los nodos alcanzables desde el nodo inicial forman una única componente conexa.
- Repetición: Se repite el proceso para todos los nodos no marcados, lo que lleva a la identificación de todas las componentes conexas del grafo.
El uso de BFS o DFS para este propósito es eficiente y permite recorrer todos los nodos de una componente antes de pasar a la siguiente, identificando claramente todas las partes del grafo que están conectadas entre sí.
¿Qué diferencias hay entre los recorridos en árboles y en grafos generales?
La principal diferencia entre los recorridos en árboles y en grafos generales es que los árboles son estructuras mucho más simples, sin ciclos, mientras que los grafos pueden tener ciclos, múltiples conexiones entre nodos y componentes desconexas. Esta distinción afecta directamente a la forma en que los algoritmos de búsqueda, como BFS y DFS, se comportan en cada caso.
- En un árbol: No existen ciclos, por lo que los algoritmos de búsqueda pueden proceder sin la necesidad de marcar nodos visitados o preocuparse por bucles. Cada nodo tiene un camino único hacia cualquier otro nodo en el árbol, lo que simplifica el recorrido.
- En un grafo general: La posibilidad de ciclos y múltiples conexiones requiere que los algoritmos manejen cuidadosamente los nodos ya visitados para evitar caer en ciclos infinitos. Además, en los grafos desconexos, los algoritmos solo podrán recorrer una parte del grafo, a menos que se ejecuten desde varios puntos iniciales.
Los recorridos en árboles son más directos y simples debido a la ausencia de ciclos y la estructura unificada, mientras que los grafos generales requieren un manejo más cuidadoso debido a su complejidad adicional.
¿Qué es un Grafo Euleriano?
Definición de un Grafo Euleriano
Un grafo euleriano es un tipo especial de grafo que permite recorrer todas sus aristas exactamente una vez, comenzando y terminando en el mismo vértice. Este concepto proviene del matemático suizo Leonhard Euler, quien resolvió el famoso problema de los puentes de Königsberg en 1736, dando origen a la teoría de grafos.
En términos más formales, un grafo es considerado euleriano si contiene un circuito euleriano, es decir, un recorrido que utiliza cada arista del grafo exactamente una vez y que termina en el vértice inicial.
Condiciones necesarias para que un grafo sea euleriano
Para determinar si un grafo es euleriano, deben cumplirse las siguientes condiciones:
- Conexión: El grafo debe ser conexo. Esto significa que existe al menos un camino entre cualquier par de vértices.
- Grado par: Todos los vértices del grafo deben tener un grado par. El grado de un vértice es el número de aristas que inciden en él.
Si alguna de estas condiciones no se cumple, el grafo no puede ser euleriano. Sin embargo, si un grafo tiene exactamente dos vértices de grado impar, es considerado un grafo semi-euleriano, ya que posee un recorrido euleriano (sin ser un circuito).
Ejemplo práctico de un grafo euleriano
Imagina un grafo con 4 vértices conectados en un cuadrado, donde cada vértice está conectado a dos vértices adyacentes. Este grafo es euleriano porque cumple con las dos condiciones mencionadas: es conexo y todos sus vértices tienen grado par (grado 2).
¿Qué es un Grafo Hamiltoniano?
Definición de un Grafo Hamiltoniano
Un grafo hamiltoniano es aquel que contiene un circuito hamiltoniano, es decir, un recorrido que visita cada vértice exactamente una vez, comenzando y terminando en el mismo vértice. Este concepto se atribuye al matemático irlandés William Rowan Hamilton, quien estudió problemas relacionados con recorridos de grafos.
A diferencia de los grafos eulerianos, donde el enfoque está en recorrer las aristas, en los grafos hamiltonianos el objetivo es visitar los vértices sin repetirlos.
Diferencias clave respecto a los grafos eulerianos
- Aristas vs Vértices: Los grafos eulerianos se centran en recorrer aristas, mientras que los hamiltonianos se enfocan en vértices.
- Condiciones: No existen condiciones estrictas basadas en el grado de los vértices para los grafos hamiltonianos, lo que los hace más difíciles de identificar.
Por lo tanto, aunque ambos tipos de grafos implican recorridos, su enfoque y propiedades son completamente diferentes.
Diferencias entre Grafos Eulerianos y Hamiltonianos
Para entender mejor las diferencias entre grafo euleriano y hamiltoniano, es útil compararlos en una tabla:
| Característica | Grafos Eulerianos | Grafos Hamiltonianos |
|---|---|---|
| Enfoque | Recorrer todas las aristas una vez | Visitar todos los vértices una vez |
| Condiciones | Conexión y grado par en todos los vértices | No existen reglas específicas basadas en grados |
| Dificultad de identificación | Relativamente fácil con reglas claras | Más complejo; no hay algoritmo único |
Ejemplos de Grafos Hamiltonianos y Eulerianos
Con los siguientes ejemplos ilustraremos la diferencia entre el grafo hamiltoniano y euleriano.
Ejemplo de un grafo euleriano
Un pentágono regular con todos sus vértices conectados a través de sus lados. En este caso, el grafo es euleriano porque cumple las condiciones de conexión y grados pares.
Ejemplo de un grafo hamiltoniano
Un triángulo equilátero con un vértice adicional conectado a dos de sus vértices. En este grafo, existe un recorrido que permite visitar cada vértice exactamente una vez y regresar al vértice inicial, cumpliendo con las características de un circuito hamiltoniano.
Aplicaciones de los Grafos Eulerianos
Problemas de rutas
Los grafos eulerianos son ampliamente utilizados en problemas de rutas óptimas, como el problema del cartero chino, donde se busca el camino más corto que recorra todas las calles de una ciudad al menos una vez.
Logística y transporte
En el ámbito logístico, los grafos eulerianos ayudan a diseñar rutas eficientes para vehículos, minimizando costos y tiempos en recorridos de entrega o recolección de mercancías.
Mantenimiento de redes
Los grafos eulerianos son útiles en el mantenimiento de redes eléctricas, hídricas y de telecomunicaciones, al permitir planificar recorridos que inspeccionen todas las conexiones con la mínima repetición posible.
Estos ejemplos ilustran la utilidad práctica de los grafos eulerianos en una variedad de contextos que van desde problemas matemáticos hasta aplicaciones en el mundo real.
Aplicaciones de los Grafos Hamiltonianos
Problemas del Viajante de Comercio
Uno de los usos más conocidos de los grafos hamiltonianos es en el problema del viajante de comercio (TSP, por sus siglas en inglés). Este problema consiste en encontrar la ruta más corta que permita a un vendedor visitar cada ciudad de una lista exactamente una vez y regresar al punto de partida.
El TSP tiene aplicaciones en logística, planificación de rutas y gestión de recursos. Por ejemplo, las empresas de reparto pueden utilizar soluciones basadas en grafos hamiltonianos para optimizar sus rutas y minimizar costos de transporte.
Resolver este problema requiere identificar un circuito hamiltoniano y, al mismo tiempo, optimizar la distancia total. Dado que el TSP es un problema NP-completo, no existe un algoritmo eficiente para resolverlo en todos los casos, pero se utilizan métodos como búsqueda exhaustiva y algoritmos aproximados.
Optimización en Redes
Los grafos hamiltonianos también se aplican en la optimización de redes, como redes de computadoras o sistemas de comunicación. En estos casos, un recorrido hamiltoniano puede garantizar que se visiten todos los nodos de una red con el menor costo posible.
Por ejemplo, en redes de sensores inalámbricos, se pueden usar circuitos hamiltonianos para asegurar que cada nodo se comunique con los demás sin redundancia, optimizando la transmisión de datos y la eficiencia energética.
Cómo Identificar un Grafo Euleriano
Condiciones matemáticas para un grafo euleriano
Un grafo se considera euleriano si cumple las siguientes condiciones matemáticas:
- Conexidad: El grafo debe ser conexo, es decir, todos los vértices deben estar conectados directa o indirectamente por al menos un camino.
- Grado par: Todos los vértices deben tener un grado par (un número par de aristas que inciden en el vértice).
Si el grafo tiene exactamente dos vértices de grado impar, no será un circuito euleriano, pero puede contener un recorrido euleriano, conocido como grafo semi-euleriano.
Ejemplo práctico de identificación
Considera un grafo con 5 vértices y las siguientes aristas: (A-B), (B-C), (C-D), (D-A), (A-C). Al analizar los grados:
- Vértice A: Grado 3
- Vértice B: Grado 2
- Vértice C: Grado 3
- Vértice D: Grado 2
Dado que dos vértices (A y C) tienen grados impares, el grafo no es euleriano, pero es semi-euleriano.
Cómo Identificar un Grafo Hamiltoniano
Métodos comunes de detección
Detectar un grafo hamiltoniano es más complicado, ya que no existen condiciones matemáticas simples como en el caso de los grafos eulerianos. Sin embargo, se pueden usar los siguientes métodos:
- Búsqueda exhaustiva: Probar todas las combinaciones posibles de recorridos para determinar si existe un circuito hamiltoniano.
- Teorema de Dirac: Si en un grafo simple con n vértices (n ≥ 3), cada vértice tiene un grado mayor o igual a n/2, entonces el grafo es hamiltoniano.
- Teorema de Ore: Si para cada par de vértices no adyacentes su grado combinado es mayor o igual a n, el grafo es hamiltoniano.
Limitaciones en la identificación
A pesar de estos métodos, detectar circuitos hamiltonianos es un problema NP-completo, lo que significa que puede requerir mucho tiempo para resolver en grafos grandes.
Algoritmos para Ciclos Eulerianos
El algoritmo de Hierholzer
El algoritmo de Hierholzer es el método más eficiente para encontrar un ciclo euleriano en un grafo. Este algoritmo funciona bajo las siguientes premisas:
- El grafo debe ser euleriano (conexión y grados pares).
- El ciclo se construye de forma iterativa, agregando aristas no visitadas hasta completar el recorrido.
Pasos del algoritmo
1. Selecciona un vértice de inicio.
2. Sigue un recorrido utilizando aristas no visitadas hasta regresar al vértice inicial.
3. Si hay aristas no visitadas, selecciona un vértice del ciclo actual con aristas disponibles y repite.
4. Fusiona los ciclos resultantes en un único ciclo euleriano.
El algoritmo tiene una complejidad de tiempo de O(E), donde E es el número de aristas del grafo, lo que lo hace eficiente.
Algoritmos para Ciclos Hamiltonianos
Búsqueda exhaustiva
Este método prueba todas las posibles combinaciones de recorridos para determinar si existe un ciclo hamiltoniano. Aunque es confiable, tiene una complejidad factorial (O(n!)), lo que lo hace impráctico para grafos grandes.
Algoritmo A*
El algoritmo A* es un método heurístico que utiliza funciones de costo para explorar de manera eficiente las posibles rutas. Se enfoca en nodos prometedores, reduciendo el tiempo de búsqueda en comparación con métodos exhaustivos.
Algoritmos aproximados
Debido a la dificultad de resolver problemas hamiltonianos, se emplean técnicas de aproximación como:
- Algoritmos genéticos: Simulan procesos evolutivos para encontrar soluciones cercanas al óptimo.
- Algoritmos de colonia de hormigas: Simulan el comportamiento de hormigas para construir soluciones mediante caminos probabilísticos.
Estas técnicas no garantizan una solución perfecta, pero son útiles en problemas prácticos donde se necesita una respuesta rápida.
Algoritmos de Recorridos de Grafos Más Conocidos
Los grafos son una estructura central en las ciencias de la computación y el análisis de redes, y para recorrerlos y encontrar rutas óptimas se han desarrollado diversos algoritmos especializados. Cada uno de estos algoritmos está diseñado para resolver problemas específicos, ya sea la búsqueda del camino más corto, la gestión de pesos negativos o la optimización de recorridos a través de heurísticas inteligentes. A continuación, se detallan algunos de los algoritmos más conocidos y cómo funcionan en diferentes contextos.
Algoritmo de Dijkstra para encontrar el camino más corto
El algoritmo de Dijkstra es uno de los métodos más conocidos para encontrar el camino más corto en un grafo. Fue desarrollado por Edsger Dijkstra en 1956 y se utiliza principalmente en grafos ponderados donde las aristas tienen pesos no negativos. El objetivo del algoritmo es encontrar la ruta de menor costo desde un nodo fuente hasta todos los demás nodos en el grafo.
El algoritmo funciona de la siguiente manera:
- Inicialización: Se asigna una distancia infinita a todos los nodos, excepto al nodo inicial, que se marca con una distancia de cero.
- Exploración: Se selecciona el nodo no visitado con la menor distancia conocida y se examinan sus vecinos. Si se encuentra un camino más corto a través de este nodo, se actualiza la distancia de los vecinos.
- Actualización: El nodo actual se marca como visitado y el proceso se repite hasta que todos los nodos han sido procesados o hasta que se alcance el nodo destino.
El algoritmo de Dijkstra garantiza encontrar el camino más corto en grafos con pesos no negativos, lo que lo hace ideal para problemas como la navegación por GPS o la optimización de redes de transporte.
Sin embargo, tiene limitaciones en presencia de pesos negativos, ya que podría no encontrar la solución correcta. Para estos casos, otros algoritmos, como el de Bellman-Ford, son más adecuados.
Algoritmo de Bellman-Ford para grafos con pesos negativos
El algoritmo de Bellman-Ford es un método alternativo al de Dijkstra, diseñado para trabajar en grafos que pueden tener pesos negativos en sus aristas. Mientras que Dijkstra no puede gestionar correctamente los pesos negativos, Bellman-Ford es capaz de encontrar el camino más corto en estos grafos, aunque con una mayor complejidad computacional.
El algoritmo sigue un enfoque de relajación de aristas:
- Inicialización: Se asigna una distancia infinita a todos los nodos, excepto al nodo fuente, que comienza con una distancia de cero.
- Relajación de aristas: Se recorre cada arista del grafo y se actualiza la distancia de los nodos si se encuentra un camino más corto. Este paso se repite V-1 veces (donde V es el número de vértices) para garantizar que todas las distancias se optimicen.
- Detección de ciclos negativos: Después de las V-1 iteraciones, el algoritmo realiza un paso adicional para detectar si hay algún ciclo negativo, lo que indicaría que no existe un camino más corto bien definido.
El algoritmo de Bellman-Ford es útil en situaciones donde pueden existir ciclos de peso negativo que afecten los cálculos del camino más corto. Un ejemplo típico es en finanzas, donde los costos pueden variar de manera que algunos caminos terminen teniendo valores negativos.
Si bien el algoritmo de Bellman-Ford es más lento que el de Dijkstra, debido a que su complejidad es de O(V*E) (donde E es el número de aristas), sigue siendo una opción sólida para grafos complejos donde los pesos negativos son comunes.
Algoritmo A* con heurísticas para búsqueda eficiente
El algoritmo A* es un algoritmo de búsqueda informada que combina las mejores características de Dijkstra y la búsqueda heurística. Es utilizado para encontrar el camino más corto de manera más eficiente que los algoritmos tradicionales, especialmente en contextos donde se puede aprovechar una heurística para guiar la búsqueda.
A* utiliza una función de costo total f(n), que es la suma de dos valores:
- g(n): El costo acumulado desde el nodo inicial hasta el nodo n.
- h(n): Una heurística que estima el costo desde el nodo n hasta el nodo objetivo.
El algoritmo A* sigue estos pasos:
- Inicialización: Se asigna al nodo inicial un valor f(n) que es igual a la heurística estimada h(n). Se coloca este nodo en una cola de prioridad.
- Exploración: Se selecciona el nodo con el menor valor de f(n), y se exploran sus vecinos. Para cada vecino, se calcula el nuevo valor de f(n) y se actualiza si se encuentra un camino más corto.
- Repetición: El proceso continúa hasta que el nodo objetivo es el que tiene el valor de f(n) más bajo, garantizando que se ha encontrado el camino más corto.
La clave del éxito de A* es la elección de una heurística adecuada. Si la heurística es informada y precisa, A* puede encontrar el camino más corto de manera mucho más rápida que los métodos tradicionales. Algunos ejemplos de heurísticas utilizadas son la distancia euclidiana o la distancia Manhattan, dependiendo del tipo de problema.
El algoritmo A* se utiliza en aplicaciones donde la eficiencia es crucial, como en juegos de video, sistemas de navegación y en la inteligencia artificial para encontrar soluciones óptimas en un espacio de búsqueda complejo.
Grafos Ponderados y Grafos con Pesos Negativos
¿Qué es un grafo ponderado?
Un grafo ponderado es una estructura de datos que se utiliza para representar un conjunto de vértices y aristas, donde cada arista tiene un valor numérico o peso asociado. Estos pesos suelen representar distancias, costos o tiempos de recorrido entre los vértices. A diferencia de los grafos no ponderados, en los cuales todas las aristas se consideran iguales, en los grafos ponderados la importancia o el impacto de una conexión puede variar según su peso.
En un grafo dirigido ponderado, las aristas tienen una dirección específica, lo que significa que el peso puede aplicarse solo en una dirección. Por otro lado, en un grafo no dirigido, las conexiones son bidireccionales, y el peso de la arista es el mismo en ambos sentidos. Esta distinción es fundamental al trabajar con problemas que involucran optimización, como el cálculo de la ruta más corta entre dos vértices.
El uso de grafos ponderados es común en aplicaciones como rutas de transporte, donde los pesos pueden representar la distancia entre ciudades o el tiempo necesario para viajar entre ellas. También se utilizan en redes de comunicaciones, donde los pesos pueden representar el costo o la capacidad de una conexión.
- Distancia: Representa la longitud o magnitud entre dos vértices.
- Tiempo: El tiempo requerido para recorrer la arista entre dos puntos.
- Costo: En aplicaciones como redes, puede representar el precio o gasto de una conexión.
Un grafo ponderado no solo conecta vértices, sino que también define la importancia relativa de cada conexión mediante el uso de pesos, lo que amplía significativamente sus aplicaciones.
¿Cómo afecta un grafo ponderado a los recorridos como BFS o DFS?
Al aplicar algoritmos de búsqueda como BFS (Breadth-First Search) o DFS (Depth-First Search) en un grafo ponderado, los pesos de las aristas juegan un papel importante en cómo se realizan los recorridos. Ambos algoritmos fueron diseñados originalmente para trabajar en grafos no ponderados, por lo que, en un grafo ponderado, sus resultados pueden no ser ideales si se busca la optimización de caminos basados en los pesos.
BFS, por ejemplo, explora todos los nodos a una misma distancia antes de avanzar a nodos más lejanos. Sin embargo, en un grafo ponderado, la distancia no siempre es lo más relevante, ya que los pesos pueden variar entre las conexiones. Si se utiliza BFS en un grafo ponderado, el algoritmo no considerará el peso de las aristas, por lo que puede no encontrar la ruta más corta en términos de costo o tiempo.
DFS, por otro lado, explora los caminos hasta su final antes de retroceder. Aunque este enfoque puede ser útil en ciertos contextos, no es adecuado para encontrar rutas óptimas en grafos ponderados, ya que DFS no tiene en cuenta los pesos de las aristas. El recorrido profundiza sin importar si una arista es "más costosa" que otra, lo que puede llevar a soluciones subóptimas.
Por lo tanto, en grafos ponderados, se utilizan algoritmos especializados para el cálculo de caminos óptimos, como:
- Algoritmo de Dijkstra: Encuentra el camino más corto desde un nodo origen a todos los demás nodos, considerando los pesos de las aristas.
- Algoritmo de Bellman-Ford: Permite encontrar el camino más corto en grafos con pesos negativos.
Mientras que BFS y DFS pueden ser útiles en grafos no ponderados, en grafos ponderados no ofrecen soluciones óptimas, lo que requiere el uso de otros algoritmos para tener en cuenta los pesos de las aristas.
¿Cómo se recorren grafos que contienen pesos negativos?
Los grafos que contienen pesos negativos presentan un desafío particular en la optimización de recorridos. Un peso negativo indica que, al atravesar una arista, el "costo" total disminuye en lugar de aumentar, lo que puede ocurrir en sistemas financieros o en modelos donde ciertos eventos pueden reducir el costo total.
En estos casos, no se puede usar el algoritmo de Dijkstra, ya que asume que todos los pesos son no negativos y puede fallar al procesar aristas con pesos negativos. En su lugar, se emplean algoritmos como:
- Bellman-Ford: Este algoritmo es capaz de manejar pesos negativos y puede detectar ciclos negativos (caminos cerrados que reducen el costo indefinidamente). Sin embargo, tiene una complejidad temporal mayor en comparación con Dijkstra.
- Floyd-Warshall: Este es un algoritmo de programación dinámica que también puede manejar pesos negativos y se utiliza para encontrar las rutas más cortas entre todos los pares de vértices en un grafo.
Un problema importante que surge al trabajar con grafos con pesos negativos es la presencia de ciclos negativos. Estos ciclos permiten reducir indefinidamente el peso total de un recorrido, lo que significa que no existe una solución de camino más corto válida. En estos casos, los algoritmos como Bellman-Ford no solo encuentran el camino más corto, sino que también detectan la existencia de ciclos negativos.
La siguiente tabla ilustra las diferencias entre los algoritmos de Dijkstra y Bellman-Ford en términos de su capacidad para manejar pesos negativos:
| Algoritmo | Soporta Pesos Negativos | Complejidad | Detección de Ciclos Negativos |
|---|---|---|---|
| Dijkstra | No | O(V²) o O(E + V log V) | No |
| Bellman-Ford | Sí | O(V * E) | Sí |
Para grafos con pesos negativos, el algoritmo de Bellman-Ford es el más adecuado debido a su capacidad para manejar este tipo de pesos y detectar ciclos negativos. Es importante elegir el algoritmo adecuado según las características del grafo para garantizar que el recorrido sea eficiente y correcto.
Recorridos Especializados en Grafos Específicos
Los grafos son estructuras fundamentales en la ciencia de la computación y las matemáticas, utilizados para modelar relaciones entre diferentes elementos. Sin embargo, existen diversos tipos de grafos que tienen características y comportamientos únicos, lo que lleva a la necesidad de aplicar algoritmos especializados para su recorrido. Esta sección se enfoca en los recorridos de tres tipos importantes de grafos: bipartitos, eulerianos y hamiltonianos, así como la influencia de los grafos planarios en la implementación de estos recorridos.
¿Qué son los grafos bipartitos y cómo se recorren?
Un grafo bipartito es un tipo de grafo en el cual sus vértices pueden dividirse en dos conjuntos disjuntos, de manera que no existen aristas que conecten vértices dentro de un mismo conjunto. Dicho de otra manera, cada arista siempre conecta un vértice del conjunto A con un vértice del conjunto B. Esta propiedad es útil en aplicaciones como la asignación de trabajos, donde un conjunto puede representar trabajadores y el otro tareas, asegurando que cada conexión (arista) respete las restricciones del problema.
Para recorrer un grafo bipartito, se utilizan métodos clásicos de recorrido como BFS (Búsqueda en Anchura) y DFS (Búsqueda en Profundidad). Sin embargo, estos recorridos se realizan prestando atención a la estructura bipartita, ya que uno de los objetivos más comunes es verificar si un grafo es bipartito o no. Para esto, se utiliza un proceso de coloreado, en el que se intenta asignar un color diferente a los vértices de los dos conjuntos.
- BFS: En BFS, se comienza desde un vértice y se colorea, por ejemplo, de rojo. A todos sus vecinos se les asigna el color azul. Posteriormente, los vecinos de los vértices azules reciben el color rojo. Si en cualquier momento se intenta colorear un vértice que ya tiene un color asignado incorrecto, el grafo no es bipartito.
- DFS: Al igual que en BFS, se asignan colores alternativos a medida que se profundiza en el grafo. La principal diferencia es que se recorre el grafo de manera más profunda antes de retroceder, lo que a veces puede ser más eficiente en ciertos casos.
Los grafos bipartitos tienen aplicaciones en muchas áreas, como el emparejamiento de conjuntos (matching) y en problemas de flujo máximo. Además, comprobar si un grafo es bipartito tiene implicaciones en la teoría de la coloración de grafos.
Recorridos en grafos eulerianos y hamiltonianos
Los grafos eulerianos y grafos hamiltonianos son dos tipos de grafos que se centran en recorridos muy específicos. Cada uno tiene propiedades y recorridos especializados que los distinguen de otros grafos.
Un grafo euleriano es aquel que contiene un ciclo que recorre todas las aristas del grafo exactamente una vez. Para que un grafo sea euleriano, debe cumplir dos condiciones:
- Todos los vértices deben tener un grado par.
- El grafo debe ser conexo, es decir, debe existir un camino entre cualquier par de vértices.
El recorrido de un grafo euleriano se realiza utilizando el Algoritmo de Fleury o el Algoritmo de Hierholzer. Estos algoritmos garantizan que se puede construir un ciclo o camino euleriano, dependiendo de si el grafo es euleriano o semi-euleriano.
Por otro lado, un grafo hamiltoniano contiene un ciclo que pasa por cada vértice exactamente una vez. A diferencia de los grafos eulerianos, no existen condiciones simples que determinen si un grafo es hamiltoniano, lo que hace que el problema de encontrar ciclos hamiltonianos sea considerablemente más difícil y computacionalmente costoso.
El recorrido de grafos hamiltonianos suele abordarse con técnicas de búsqueda como:
- Backtracking: Una técnica que intenta construir un ciclo paso a paso y retrocede cuando encuentra un callejón sin salida.
- Heurísticas: Como el Algoritmo de Vecino Más Cercano (Nearest Neighbor), que intenta encontrar soluciones aproximadas en problemas NP-completos como este.
Comparativamente, los recorridos en grafos eulerianos son más simples de determinar, mientras que los hamiltonianos representan un desafío mayor, sobre todo en grafos de gran tamaño o complejidad.
¿Cómo afectan los grafos planarios a la implementación de los recorridos?
Los grafos planarios son aquellos que pueden dibujarse en un plano sin que ninguna de sus aristas se cruce. Esta propiedad tiene implicaciones significativas en la implementación de algoritmos de recorrido, ya que los grafos planarios permiten optimizaciones en el almacenamiento de información y en el procesamiento de los vértices y aristas.
Uno de los problemas clave en los grafos planarios es la planaridad, es decir, determinar si un grafo puede representarse sin cruces. Los algoritmos como el Algoritmo de Kuratowski y el Algoritmo de Fraysseix-Rosenstiehl son esenciales para verificar esta propiedad.
- Recorridos más eficientes: Debido a la estructura de los grafos planarios, algunos recorridos, como el DFS y BFS, pueden realizarse con mayor eficiencia en términos de tiempo y espacio.
- Algoritmos de optimización: Los grafos planarios permiten optimizaciones en problemas como la triangulación, donde se pueden reducir las aristas innecesarias sin afectar el recorrido.
- Visualización: Un beneficio clave de los grafos planarios es que son más fáciles de visualizar, lo que facilita la implementación de algoritmos de recorrido en aplicaciones gráficas o de diseño.
En la práctica, los grafos planarios también tienen aplicaciones en problemas de redes y circuitos eléctricos, donde las conexiones deben minimizarse para evitar cruces innecesarios. Además, las propiedades geométricas de estos grafos facilitan la creación de algoritmos de particionamiento y minimización.
A continuación, una tabla comparativa que muestra cómo los grafos planarios influyen en los diferentes tipos de recorridos:
| Tipo de Grafo | Impacto de la Planaridad | Optimización en Recorridos |
|---|---|---|
| Grafo Bipartito | Bajo impacto, aunque puede facilitar visualización | Posible optimización en particionamiento |
| Grafo Euleriano | Planaridad puede simplificar el ciclo euleriano | Mejora en la determinación de conexiones |
| Grafo Hamiltoniano | Mayor impacto, ya que minimiza caminos alternativos | Optimización en la búsqueda de ciclos |
Los grafos planarios no solo ofrecen una ventaja en términos de eficiencia y claridad en los recorridos, sino que también permiten optimizaciones específicas según el tipo de grafo que se esté trabajando.
Recorridos en Grafos Conexos y Dirigidos Acíclicos (DAG)
Los grafos juegan un papel fundamental en la resolución de problemas complejos, ya sea en redes, análisis de flujos, o en la optimización de procesos.
Existen dos tipos de grafos que presentan características específicas y requieren algoritmos especializados para su recorrido: los grafos conexos y los grafos dirigidos acíclicos (DAG). En esta sección, exploraremos cómo estas propiedades afectan los algoritmos de recorrido y cómo se deben adaptar los métodos clásicos de recorrido.
¿Qué es un grafo conexo y cómo afecta a los recorridos?
Un grafo conexo es un grafo no dirigido en el que existe un camino entre cada par de vértices. En otras palabras, no hay vértices aislados o grupos de vértices desconectados entre sí.
Esta propiedad es fundamental, ya que garantiza que el grafo pueda recorrerse completamente desde cualquier vértice, sin la necesidad de cambiar de componente.
Los recorridos en un grafo conexo son más eficientes porque se asegura que todos los vértices puedan ser visitados en un solo recorrido. Los dos algoritmos principales para este tipo de grafos son:
- DFS (Búsqueda en Profundidad): Este algoritmo recorre el grafo adentrándose en cada vértice a lo largo de las aristas hasta llegar a un callejón sin salida, y luego retrocede. En grafos conexos, el DFS garantiza la visita a todos los vértices sin necesidad de reiniciar el recorrido en otro componente.
- BFS (Búsqueda en Anchura): Este algoritmo explora todos los vértices vecinos de un vértice antes de continuar con sus vecinos más lejanos. En un grafo conexo, el BFS se realiza sin interrupciones, lo que garantiza la visita a todos los vértices de manera secuencial.
La conectividad de un grafo afecta directamente la complejidad y el comportamiento de los algoritmos de recorrido:
- Eficiencia: En un grafo conexo, los algoritmos no necesitan reiniciarse para recorrer componentes separados. Esto reduce el tiempo de ejecución.
- Aplicaciones: Los grafos conexos son útiles en problemas de redes de transporte, donde es crucial garantizar que todos los puntos estén conectados, y en redes de comunicaciones, donde la falta de conectividad puede significar interrupciones en el servicio.
- Propiedades: En un grafo no conexo, existen múltiples componentes. En cambio, un grafo conexo asegura un solo componente, simplificando el análisis y recorrido.
Comparar grafos conexos y no conexos puede ayudar a entender las diferencias en la implementación de recorridos:
| Tipo de Grafo | Conectividad | Impacto en Recorridos |
|---|---|---|
| Conexo | Un solo componente | Recorridos eficientes sin reiniciar el algoritmo |
| No Conexo | Varios componentes desconectados | Se requieren múltiples recorridos para cubrir todo el grafo |
Entonces ahora puedes entender cuando un grafo es conexo, ya que, un grafo conexo permite recorridos más simples y directos, reduciendo la complejidad de los algoritmos al no tener que preocuparse por componentes aislados.
¿Cómo afectan los grafos dirigidos acíclicos (DAG) a los algoritmos de recorrido?
Un grafo dirigido acíclico (DAG) es un grafo dirigido que no contiene ciclos, lo que significa que no es posible comenzar en un vértice y, siguiendo las aristas dirigidas, regresar al mismo vértice. Los DAG son fundamentales en la informática y tienen una amplia variedad de aplicaciones, desde la programación de tareas hasta la optimización de flujos de trabajo.
El hecho de que un DAG sea acíclico tiene profundas implicaciones en los algoritmos de recorrido, ya que se garantiza que el grafo tiene una dirección de flujo clara, sin bucles que compliquen el proceso de recorrido.
- Ordenación Topológica: Una de las aplicaciones más importantes de los DAG es la ordenación topológica, que consiste en organizar los vértices del grafo de manera que para cada arista dirigida u → v, el vértice u aparezca antes que el vértice v en el orden. Este recorrido es clave en problemas como la planificación de tareas, donde algunas tareas deben realizarse antes que otras.
- Detección de dependencias: En un DAG, las dependencias entre vértices (como tareas o procesos) pueden ser modeladas de forma eficiente, ya que la estructura acíclica impide que una tarea dependa de sí misma directa o indirectamente.
- Recorridos DFS y BFS: Aunque los algoritmos DFS y BFS se pueden aplicar en un DAG, la ausencia de ciclos permite optimizaciones adicionales, como la terminación anticipada cuando se detecta que se ha alcanzado un vértice sin salidas.
El hecho de que un DAG no contenga ciclos significa que ciertos problemas de recorrido pueden simplificarse considerablemente. Por ejemplo, en problemas de caminos más largos o de optimización de rutas, el recorrido en un DAG tiene la ventaja de no tener que lidiar con bucles, lo que reduce la complejidad.
Además, los DAG se utilizan en:
- Compiladores: Los DAG se utilizan para optimizar la ejecución de programas, donde las dependencias entre variables y operaciones deben ser resueltas sin generar ciclos.
- Redes de proyectos: En la planificación de proyectos, los DAG permiten modelar dependencias entre tareas, facilitando la programación eficiente de actividades sin conflictos.
- Flujos de trabajo: En sistemas de procesamiento de datos, los DAG son cruciales para modelar el flujo de información sin generar bucles que puedan crear inconsistencias.
La siguiente tabla muestra las diferencias clave entre un grafo dirigido con ciclos y un grafo dirigido acíclico (DAG):
| Tipo de Grafo | Existencia de Ciclos | Impacto en Algoritmos |
|---|---|---|
| Grafo Dirigido con Ciclos | Puede tener ciclos | Complica la resolución de dependencias y la ordenación topológica |
| DAG | No contiene ciclos | Optimiza la planificación de tareas y dependencias |
Los grafos dirigidos acíclicos (DAG) permiten la implementación de algoritmos más eficientes para la resolución de dependencias y la optimización de tareas, eliminando la complejidad que presentan los ciclos en grafos dirigidos. La estructura clara y dirigida de los DAG es una ventaja en aplicaciones que requieren un flujo de información o tareas sin retrocesos o bucles.
Optimización de Recorridos en Grafos
Los grafos son estructuras de datos fundamentales en la informática, utilizados para modelar todo tipo de relaciones y redes, como conexiones en redes sociales, rutas de transporte, e incluso interacciones moleculares. La optimización de los recorridos en grafos es un tema crucial cuando se trata de grandes volúmenes de datos o redes distribuidas, ya que el tamaño y la complejidad de estas estructuras pueden ralentizar significativamente los procesos de búsqueda y análisis. A continuación, abordaremos cómo se optimizan estos recorridos, especialmente en contextos de redes grandes o distribuidas, y cómo la paralelización puede mejorar su rendimiento.
¿Cómo se optimizan los recorridos de grafos en grafos muy grandes o en redes distribuidas?
La optimización de los recorridos en grafos grandes o distribuidos es un desafío clave debido a la inmensa cantidad de nodos y aristas que pueden estar involucrados. Existen varias técnicas y enfoques que se emplean para mejorar la eficiencia de estos recorridos.
- Algoritmos de poda: Estos algoritmos eliminan ciertos caminos o nodos que no son relevantes para el objetivo del recorrido, reduciendo el espacio de búsqueda.
- Heurísticas de búsqueda: Métodos como A\* o búsqueda greedy ayudan a priorizar ciertos caminos que tienen más probabilidad de llevar a una solución, reduciendo así el tiempo total de búsqueda.
- Algoritmos jerárquicos: Dividir el grafo en secciones más pequeñas y recorrer estas sub-secciones de manera eficiente puede optimizar los recorridos en grafos extremadamente grandes.
Otra técnica ampliamente utilizada para optimizar los recorridos en redes distribuidas es el almacenamiento en caché de caminos previos. Si un camino entre dos nodos ya ha sido calculado en un recorrido anterior, almacenarlo en caché evita la necesidad de volver a calcularlo, reduciendo significativamente el tiempo de procesamiento.
Cuando se trata de redes distribuidas, donde el grafo puede estar dividido en múltiples nodos de computación, es importante considerar la latencia de la comunicación entre nodos. Aquí, el enfoque de recorrido local (donde cada nodo del grafo intenta resolver las subestructuras locales antes de comunicarse con otros nodos de la red) puede mejorar el rendimiento al reducir la necesidad de enviar datos a través de la red.
Las estrategias para optimizar recorridos en grafos grandes o distribuidos incluyen:
- Uso de algoritmos de poda para eliminar caminos innecesarios.
- Aplicación de heurísticas para priorizar ciertos caminos.
- División del grafo mediante algoritmos jerárquicos.
- Almacenamiento en caché de caminos previos.
- Minimización de la latencia en redes distribuidas.
Estas técnicas son fundamentales para mejorar la eficiencia en grafos de gran escala, donde el número de nodos y aristas puede ser inmanejable sin una optimización adecuada.
¿Cómo se puede paralelizar los recorridos de grafos para mejorar el rendimiento en grandes conjuntos de datos?
La paralelización de recorridos en grafos es un enfoque esencial para lidiar con grafos grandes y mejorar el rendimiento. Los grafos, debido a su estructura altamente interconectada, permiten que ciertos algoritmos sean divididos en tareas independientes que pueden ejecutarse en paralelo. Esto no solo reduce el tiempo de ejecución, sino que también aprovecha al máximo los recursos de hardware, como CPU multi-núcleo o GPU.
Existen varias técnicas para paralelizar eficientemente los recorridos de grafos:
- División de nodos y aristas: Una de las formas más sencillas de paralelización es dividir el grafo en subgrafos más pequeños y ejecutar los algoritmos de recorrido en paralelo en cada subgrafo.
- Algoritmos de propagación en paralelo: Estos algoritmos funcionan bien en grafos distribuidos y permiten que la información se propague desde varios nodos de manera simultánea. Un ejemplo común es el algoritmo de propagación de etiquetas, que se utiliza para encontrar comunidades en redes.
- Exploración en ancho o en profundidad paralela: Al paralelizar algoritmos de recorrido en amplitud (BFS) o en profundidad (DFS), se pueden procesar múltiples caminos o nodos al mismo tiempo, reduciendo el tiempo total de recorrido.
La clave de la paralelización eficiente es evitar que los procesos se bloqueen mutuamente o que esperen a que otros procesos terminen antes de continuar. Para lograr esto, se puede emplear estructuras de sincronización como barreras y exclusión mutua (mutex), aunque esto introduce cierta sobrecarga.
| Técnica | Ventajas | Desventajas |
|---|---|---|
| División de nodos | Facilita la paralelización básica | Puede generar desequilibrio en la carga de trabajo |
| Propagación en paralelo | Alta eficiencia en redes distribuidas | Comunicación constante entre nodos |
| BFS/DFS paralelos | Permite explorar múltiples rutas a la vez | Complicado de sincronizar correctamente |
En cuanto a la infraestructura, el uso de GPU es una tendencia creciente en la paralelización de recorridos de grafos. Las GPUs, debido a su naturaleza masivamente paralela, son capaces de procesar miles de operaciones de manera simultánea, lo que las hace ideales para manejar grafos de gran escala.
La paralelización de los recorridos en grafos ofrece una mejora considerable en términos de rendimiento y escalabilidad. Al aplicar estos enfoques, es posible reducir significativamente los tiempos de cómputo en grandes conjuntos de datos, permitiendo un análisis más rápido y eficiente de redes complejas.
Evitar Nodos Repetidos y Mejorar la Eficiencia
Cuando trabajamos con grafos, uno de los mayores desafíos es evitar la visita repetida de nodos. Esto es fundamental para mejorar la eficiencia de cualquier algoritmo de recorrido. Al no gestionar adecuadamente este problema, el tiempo de ejecución y la eficiencia del algoritmo se pueden ver gravemente afectados, especialmente en grafos grandes o complejos. A continuación, exploramos distintas técnicas que permiten manejar este inconveniente.
¿Qué técnicas se pueden usar para evitar visitar nodos ya explorados en un recorrido de grafo?
Existen varias técnicas eficientes que ayudan a evitar la repetición de nodos en el recorrido de grafos. A continuación, veremos algunas de las más utilizadas:
Una de las técnicas más comunes es el uso de una estructura de datos auxiliar, generalmente un conjunto o array booleano, que almacena los nodos que ya han sido visitados. De esta forma, cada vez que el algoritmo se enfrenta a un nodo, primero revisa si está en la lista de nodos visitados.
- Estructura de marcado: Mantener un array booleano donde cada índice representa un nodo, y el valor indica si ese nodo ha sido visitado. De esta manera, se puede acceder en tiempo constante O(1) para verificar si un nodo ha sido explorado.
- Tabla Hash o Set: Utilizar una tabla hash o conjunto (set) que permita almacenar los nodos ya visitados y consultarlos rápidamente. Esto es muy útil cuando los nodos no pueden representarse como índices, por ejemplo, en grafos con nodos etiquetados, siendo conocidos como grafo etiquetado.
- Modificación del grafo: En algunos casos, se puede optar por modificar directamente el grafo, eliminando o marcando los nodos que ya han sido visitados, aunque esta técnica es más invasiva y menos flexible.
Además, en el contexto de algoritmos como el DFS (Depth First Search) o BFS (Breadth First Search), la gestión de nodos visitados se vuelve esencial para evitar ciclos infinitos o visitas innecesarias, lo que impacta directamente en la complejidad temporal del algoritmo.
¿Cómo se evita la repetición de nodos en un grafo con múltiples aristas entre los mismos vértices?
En grafos donde existen múltiples aristas entre los mismos vértices, puede ocurrir que un nodo sea accesible por diferentes rutas. Para manejar este escenario, se utilizan algunas estrategias clave que garantizan que cada nodo se visite una sola vez, sin importar cuántas conexiones existan entre los vértices.
Un enfoque simple es, nuevamente, el uso de una estructura de datos de nodos visitados. A continuación, presentamos otras soluciones más específicas:
- Eliminar aristas duplicadas: Antes de iniciar el recorrido, se puede limpiar el grafo eliminando aristas redundantes entre los nodos. Esta técnica es eficaz en grafos estáticos donde las relaciones no cambian con frecuencia.
- Gestionar rutas alternativas: En lugar de eliminar aristas, se puede utilizar una estructura para almacenar todas las rutas posibles hacia un nodo, asegurándose de que se visite solo la ruta óptima o preferida.
- Uso de algoritmos especializados: Algunos algoritmos, como Dijkstra o A* (A estrella), están diseñados específicamente para encontrar la ruta más corta entre dos nodos y manejar grafos con múltiples aristas entre los mismos vértices de manera eficiente.
Estos enfoques son fundamentales para evitar que el algoritmo se quede atrapado en bucles o pierda tiempo recorriendo caminos redundantes, lo que es especialmente problemático en grafos ponderados donde la existencia de múltiples aristas con diferentes pesos es común.
¿Cómo manejar grafos dispersos frente a grafos densos en términos de recorrido?
La estructura del grafo influye significativamente en la eficiencia de los algoritmos de recorrido. Un grafo puede ser disperso o denso dependiendo del número de aristas en relación con el número de vértices. La gestión de estos dos tipos de grafos requiere estrategias diferentes para garantizar un recorrido eficiente.
Un grafo disperso es aquel en el que el número de aristas es bajo en comparación con la cantidad de vértices. Para estos grafos, las técnicas más eficaces son:
- Listas de adyacencia: Utilizar una lista de adyacencia es ideal para grafos dispersos, ya que solo almacena las aristas que existen, lo que reduce significativamente el uso de memoria y mejora la eficiencia del recorrido.
- Búsqueda en anchura (BFS): Dado que un grafo disperso tiene menos aristas, BFS suele ser eficiente, ya que explora nodo por nodo de manera ordenada, sin revisitar muchas veces las conexiones existentes.
- Optimización de búsqueda: Utilizar técnicas como recorte de búsqueda (pruning) puede ser útil en grafos dispersos donde muchas de las aristas no llevan a ninguna parte relevante.
Por otro lado, en un grafo denso, donde existe una gran cantidad de aristas, el desafío principal es evitar el sobrecosto computacional de revisar muchas conexiones innecesarias:
- Matrices de adyacencia: En estos casos, una matriz de adyacencia puede ser más adecuada, ya que permite acceder directamente a las conexiones entre nodos en tiempo constante O(1), aunque con un mayor costo en términos de memoria.
- DFS optimizado: En grafos densos, un DFS (Depth First Search) optimizado puede ser más eficiente, ya que permite explorar cada rama del grafo hasta su profundidad, evitando la necesidad de recorrer repetidamente todas las aristas.
- Heurísticas de recorrido: Utilizar algoritmos con heurísticas, como A*, puede mejorar la eficiencia en grafos densos, al enfocarse solo en las rutas más prometedoras y evitar caminos que no aportan a la solución.
La elección del algoritmo adecuado depende en gran medida de la estructura del grafo, y es esencial ajustar tanto el algoritmo como la representación del grafo (listas o matrices de adyacencia) para maximizar la eficiencia en el recorrido.
Que son los grafos en programacion
En el ámbito de la programación, los grafos son estructuras de datos utilizadas para modelar relaciones entre elementos.
Un grafo en programación es una estructura de datos que representa relaciones entre un conjunto de elementos llamados nodos (o vértices) y las conexiones entre ellos, conocidas como aristas (o edges).
Tipos de Grafos en Programación
- Grafos dirigidos: Las aristas tienen una dirección, como en un grafo que representa el tráfico en calles de un solo sentido.
- Grafos no dirigidos: Las aristas no tienen dirección, como en un grafo que representa relaciones de amistad.
- Grafos ponderados: Cada arista tiene un peso, útil en problemas como encontrar la ruta más corta.
- Grafos no ponderados: Las aristas no tienen peso y simplemente representan conexiones.
- Grafos cíclicos: Contienen al menos un ciclo, es decir, un camino que regresa al vértice de inicio.
- Grafos acíclicos: No contienen ciclos. Ejemplo común: árboles.
Representación de Grafos en Programación
En programación, los grafos se pueden representar de diferentes maneras, dependiendo del caso de uso y los requisitos de rendimiento:
Matriz de Adyacencia
Se utiliza una matriz bidimensional para representar las conexiones entre nodos. Si hay una conexión entre el nodo i y el nodo j, la celda [i][j] tiene un valor (por ejemplo, 1 para grafos no ponderados o el peso de la conexión para grafos ponderados).
# Ejemplo de matriz de adyacencia para un grafo con 3 nodos
grafo = [
[0, 1, 1],
[1, 0, 0],
[1, 0, 0]
]
Ventaja: Fácil acceso a las conexiones.
Desventaja: Utiliza más memoria, especialmente para grafos dispersos.
Lista de Adyacencia
Se utiliza un diccionario o un array de listas para almacenar las conexiones de cada nodo.
# Ejemplo de lista de adyacencia
grafo = {
0: [1, 2],
1: [0],
2: [0]
}
Ventaja: Más eficiente en memoria para grafos dispersos.
Desventaja: Puede ser más lento para acceder a conexiones específicas.
Operaciones Comunes en Grafos
- Búsqueda: Identificar si un nodo está conectado a otro (por ejemplo, usando BFS o DFS).
- Camino más corto: Encontrar la ruta de menor costo entre dos nodos (usando algoritmos como Dijkstra o Bellman-Ford).
- Conectividad: Determinar si todos los nodos están conectados en un único componente.
- Detección de ciclos: Identificar si el grafo contiene ciclos.
Algoritmos Relacionados con Grafos
Los algoritmos en grafos son fundamentales en programación, y algunos de los más importantes son:
Búsqueda en Amplitud (BFS) y Búsqueda en Profundidad (DFS)
Estas técnicas se utilizan para recorrer grafos:
- BFS: Explora nivel por nivel, útil para encontrar el camino más corto en grafos no ponderados.
- DFS: Explora en profundidad, útil para detectar ciclos o recorrer grafos de forma completa.
# Ejemplo básico de BFS
from collections import deque
def bfs(grafo, inicio):
visitados = set()
cola = deque([inicio])
while cola:
nodo = cola.popleft()
if nodo not in visitados:
visitados.add(nodo)
cola.extend(grafo[nodo])
return visitados
Algoritmo de Dijkstra
Este algoritmo encuentra el camino más corto desde un nodo de inicio a todos los demás nodos en un grafo ponderado.
# Ejemplo básico de Dijkstra
import heapq
def dijkstra(grafo, inicio):
distancias = {nodo: float('inf') for nodo in grafo}
distancias[inicio] = 0
cola_prioridad = [(0, inicio)]
while cola_prioridad:
(dist_actual, nodo) = heapq.heappop(cola_prioridad)
for vecino, peso in grafo[nodo].items():
nueva_dist = dist_actual + peso
if nueva_dist < distancias[vecino]:
distancias[vecino] = nueva_dist
heapq.heappush(cola_prioridad, (nueva_dist, vecino))
return distancias
Aplicaciones de Grafos en Programación
Los grafos son increíblemente versátiles y tienen aplicaciones prácticas en múltiples áreas:
- Redes sociales: Modelar relaciones entre usuarios.
- Sistemas de transporte: Optimizar rutas en redes de carreteras o transporte público.
- Redes de computadoras: Representar conexiones y optimizar el enrutamiento de datos.
- Problemas biológicos: Análisis de redes genéticas y estructuras moleculares.
Implementación de Recorridos en Lenguajes de Programación
Los recorridos de grafos en programacion son una parte esencial de los algoritmos utilizados en el análisis y resolución de problemas en estructuras de datos.
Dos de los algoritmos más conocidos para realizar recorridos en grafos son el BFS (Breadth-First Search) y el DFS (Depth-First Search).
Estos algoritmos son ampliamente implementados en lenguajes como Python, C++ y Java debido a su eficiencia y flexibilidad.
A continuación, veremos cómo se pueden implementar estos algoritmos y las herramientas clave necesarias para ello.
¿Cómo se implementan BFS y DFS en lenguajes de programación como Python, C++ o Java?
La implementación de los algoritmos BFS y DFS puede variar ligeramente según el lenguaje de programación, pero los principios básicos permanecen iguales. A continuación, examinamos cómo se realizan en tres lenguajes de programación populares: Python, C++ y Java.
BFS se basa en un enfoque de búsqueda por niveles. Empieza por un nodo inicial y explora todos sus vecinos antes de pasar al siguiente nivel. DFS, por otro lado, sigue una rama del grafo hasta el final antes de retroceder y explorar otras ramas.
Implementación de BFS:
- Python: Se suele usar una cola (`queue.Queue`) para gestionar el orden de visita de los nodos.
- C++: Se utiliza la STL (Standard Template Library), en particular, la clase `queue` para gestionar la lista de nodos.
- Java: Se usa `LinkedList` como cola, gracias a su capacidad de permitir la inserción y eliminación de elementos en ambos extremos.
Implementación de DFS:
- Python: Aquí, una pila puede ser representada fácilmente utilizando una lista (`list`), debido a la capacidad de Python para manejar operaciones de apilado y desapilado.
- C++: Se utiliza la STL nuevamente, pero esta vez con la estructura `stack` para simular el comportamiento de una pila.
- Java: `Stack` es una clase incorporada que facilita la implementación de DFS en este lenguaje.
| Lenguaje | BFS (Estructura) | DFS (Estructura) |
|---|---|---|
| Python | queue.Queue | list (como pila) |
| C++ | queue (STL) | stack (STL) |
| Java | LinkedList | Stack |
¿Cómo utilizar colas y pilas en la implementación de BFS y DFS?
En los algoritmos BFS y DFS, las estructuras de datos son la clave para gestionar el flujo de los recorridos. En particular, las colas y pilas son las más utilizadas para facilitar el proceso de exploración de los nodos en un grafo.
Para BFS, una cola es fundamental. Esto se debe a que en un recorrido por niveles, se exploran primero todos los nodos de un nivel antes de avanzar al siguiente. La estructura de cola permite insertar nodos en el fondo y extraerlos desde el frente, lo que respeta el orden de nivel necesario.
Pasos para implementar BFS utilizando colas:
- Inicializar una cola vacía.
- Agregar el nodo inicial a la cola.
- Mientras la cola no esté vacía, extraer el nodo frontal.
- Visitar sus vecinos y agregarlos a la cola.
Por otro lado, en DFS se utiliza una pila porque este algoritmo profundiza en una rama antes de retroceder. La pila respeta el principio LIFO (Last In, First Out), lo que permite volver sobre nodos anteriores a medida que se retrocede.
Pasos para implementar DFS utilizando pilas:
- Inicializar una pila vacía.
- Agregar el nodo inicial a la pila.
- Mientras la pila no esté vacía, extraer el nodo superior.
- Visitar sus vecinos y agregarlos a la pila en orden inverso para seguir explorando la rama más profunda.
Dificultades comunes al implementar recorridos de grafos en sistemas reales
La implementación de recorridos de grafos en sistemas reales presenta varios desafíos. Estos problemas a menudo se deben a la complejidad del sistema, la escala de los grafos y la falta de familiaridad con ciertas estructuras de datos o técnicas de optimización.
Entre las dificultades más comunes se incluyen:
- Escalabilidad: A medida que los grafos crecen en tamaño, la cantidad de memoria y tiempo de procesamiento requerido aumenta considerablemente. Algoritmos como BFS y DFS pueden ser ineficientes en grandes grafos si no se optimizan correctamente.
- Control de ciclos: En grafos cíclicos, es crucial evitar que el algoritmo entre en un ciclo infinito. Para solucionar esto, es necesario mantener un registro de los nodos visitados. Olvidar este paso puede llevar a problemas graves de rendimiento.
- Optimización de memoria: Ambos algoritmos pueden consumir grandes cantidades de memoria en sistemas con recursos limitados. Por ejemplo, DFS puede profundizar tanto que la pila crezca demasiado, causando errores de desbordamiento en lenguajes con manejo limitado de memoria como C++.
- Manejo de grafos no conectados: A veces, los grafos no están completamente conectados. En estos casos, es necesario asegurarse de que todos los nodos sean visitados, incluso si pertenecen a componentes desconectados.
- Problemas de sincronización: En sistemas distribuidos o paralelos, implementar BFS o DFS de manera eficiente requiere controlar la sincronización entre diferentes hilos o procesos. Esto puede ser complicado y puede llevar a errores si no se gestiona correctamente.
Para superar estas dificultades, es importante estar familiarizado con técnicas de optimización específicas del lenguaje y del sistema. Además, en muchos casos, se requiere ajustar el algoritmo o utilizar versiones modificadas como BFS con heurísticas o DFS con límites de profundidad, dependiendo del problema en cuestión.
Recorridos Avanzados y Modificados
Los algoritmos de recorrido de grafos, como el BFS y el DFS, son técnicas fundamentales en el análisis y solución de problemas complejos. Sin embargo, en algunos casos, los problemas pueden requerir modificaciones avanzadas o nuevas estrategias para mejorar la eficiencia o para resolver problemas específicos, como puzzles o laberintos. En esta sección, exploramos algunos de los recorridos avanzados y modificados, como los recorridos bidireccionales y las versiones modificadas del DFS, que pueden adaptarse para casos más específicos.
¿Qué son los recorridos bidireccionales y cuándo es conveniente utilizarlos?
El recorrido bidireccional es una extensión de los algoritmos tradicionales de búsqueda, como el BFS. En lugar de explorar el grafo desde un solo punto, se inician dos búsquedas simultáneas: una desde el nodo de partida y otra desde el nodo de destino. El objetivo es que estas búsquedas se encuentren en algún punto intermedio, reduciendo el número de nodos que deben ser explorados para encontrar una solución.
Este tipo de recorrido es especialmente eficiente en grafos de gran tamaño, ya que en lugar de explorar todo el espacio de búsqueda desde un único punto, se exploran dos áreas más pequeñas que eventualmente convergen. Esto reduce el tiempo de ejecución, particularmente en casos donde el grafo es extenso o denso.
Ventajas de utilizar recorridos bidireccionales:
- Reducción significativa del espacio de búsqueda: Al reducir a la mitad la cantidad de nodos que se exploran, el rendimiento mejora de manera notable.
- Aplicaciones en problemas de búsqueda de rutas: Es muy útil en problemas donde se necesita encontrar la ruta más corta entre dos puntos, como en algoritmos de redes o en sistemas de navegación.
- Eficiencia en grafos grandes: Cuando el grafo tiene una gran cantidad de nodos, el recorrido bidireccional puede ser una alternativa mucho más eficiente que un BFS tradicional.
El mejor escenario para utilizar este enfoque es cuando se conoce tanto el punto de partida como el punto de destino, y el objetivo es encontrar la ruta más corta entre ellos. En estos casos, un recorrido bidireccional puede ofrecer una mejora considerable en comparación con los algoritmos unidireccionales tradicionales.
| Tipo de Recorrido | Unidireccional (BFS/DFS) | Bidireccional |
|---|---|---|
| Espacio de Búsqueda | Explora todo desde un solo punto | Explora desde dos puntos (inicio y fin) |
| Tiempo de Ejecución | Mayor, en grafos grandes | Menor, debido a la reducción del espacio de búsqueda |
| Uso Común | Búsqueda en amplitud o profundidad | Rutas cortas en grafos grandes o densos |
¿Cómo se puede modificar un recorrido DFS para resolver problemas de laberintos o puzzles?
El DFS modificado es una técnica eficaz para resolver problemas como laberintos y puzzles. En su forma básica, el algoritmo DFS explora profundamente una rama del grafo hasta que no puede avanzar más, momento en el que retrocede y explora otras ramas. Sin embargo, en problemas como los laberintos, es necesario introducir ciertas modificaciones que permitan mejorar su rendimiento y precisión.
Un laberinto o puzzle puede considerarse un grafo donde cada intersección es un nodo y cada camino es una arista. El DFS modificado puede ser utilizado para encontrar una solución a este problema si se le añaden ciertas características, como la detección de ciclos y la optimización del recorrido.
Modificaciones clave para resolver laberintos:
- Control de nodos visitados: Es crucial mantener un registro de los nodos que ya se han visitado para evitar entrar en un ciclo infinito dentro del laberinto.
- Optimización de la búsqueda: El DFS clásico sigue una rama hasta el final, pero en los laberintos puede ser útil limitar la profundidad de la búsqueda o usar heurísticas que guíen el recorrido hacia la solución de manera más eficiente.
- Uso de retroceso: En un puzzle, si el DFS llega a un camino sin salida, debe retroceder correctamente y explorar otras ramas, algo que se puede lograr fácilmente con una pila.
El DFS modificado es ideal para puzzles en los que se debe explorar exhaustivamente todas las posibles soluciones, como en el caso de laberintos complejos. Aunque el DFS tradicional puede quedarse atascado en ciclos o repetir rutas, la gestión adecuada de nodos visitados permite optimizar el algoritmo para resolver este tipo de problemas.
¿Cómo se aplica DFS modificado para resolver problemas de coloración de grafos?
El problema de la coloración de grafos es un desafío común en teoría de grafos, en el que se busca asignar colores a los nodos de un grafo de manera que no haya dos nodos adyacentes con el mismo color. Este problema es fundamental en planificación de horarios, asignación de tareas y diseño de redes, entre otros.
El DFS modificado se utiliza frecuentemente para resolver problemas de coloración, ya que permite explorar diferentes configuraciones de colores en un grafo. La idea es que el DFS explore todas las posibles asignaciones de colores, retrocediendo cuando encuentre conflictos y continuando con otras posibles soluciones.
Pasos para aplicar DFS modificado en la coloración de grafos:
- Inicializar los colores: Al comenzar, ningún nodo tiene un color asignado. Se elige un conjunto de colores disponibles.
- Aplicar DFS: El DFS explora un nodo, le asigna un color y continúa con los nodos adyacentes. Si no se puede asignar un color a un nodo (porque todos los colores posibles ya están asignados a sus vecinos), el DFS retrocede para probar una nueva combinación.
- Resolver conflictos: Si un nodo no puede ser coloreado, el DFS retrocede y asigna un nuevo color a los nodos anteriores, buscando una configuración válida.
- Optimización: Se pueden introducir heurísticas que guíen el DFS para elegir colores que maximicen las probabilidades de éxito, reduciendo el tiempo de búsqueda.
En la práctica, el DFS modificado para la coloración de grafos se combina a menudo con técnicas como el backtracking para evitar asignaciones de colores que resulten en conflictos. Este enfoque garantiza que el algoritmo encuentre una solución válida, siempre que la coloración sea posible.
Además, el DFS también se puede usar para determinar el número cromático de un grafo, que es el número mínimo de colores necesarios para colorear un grafo sin conflictos. El uso del DFS modificado permite explorar todas las posibles configuraciones de colores y encontrar la solución óptima.
Desafíos en Grafos Muy Grandes
Cuando trabajamos con grafos muy grandes, surgen varios desafíos técnicos que pueden afectar la eficiencia de los algoritmos de recorrido. Uno de los problemas más críticos es la sobrecarga de memoria, especialmente cuando el grafo tiene millones o miles de millones de nodos y aristas. Esta situación puede llevar a un agotamiento de la memoria RAM e impactar negativamente en el rendimiento del sistema. En esta sección, analizamos cómo detectar y resolver los problemas relacionados con la sobrecarga de memoria en los recorridos de grafos muy grandes.
¿Cómo detectar y resolver problemas de sobrecarga de memoria en recorridos de grafos muy grandes?
La sobrecarga de memoria ocurre cuando los algoritmos de recorrido, como bfs (Búsqueda en Amplitud) y Búsqueda en profundidad (dfs), almacenan una gran cantidad de nodos y aristas en la memoria, lo que eventualmente supera la capacidad del sistema. La detección temprana y el manejo adecuado de este problema son cruciales para evitar caídas del sistema o tiempos de ejecución extremadamente largos.
Pasos para detectar problemas de sobrecarga de memoria:
- Monitoreo del uso de memoria: La primera señal de alerta es un uso excesivo de la memoria RAM. Es posible monitorear este uso mediante herramientas como htop o psutil (en Python) para observar el crecimiento en tiempo real del consumo de memoria durante la ejecución del algoritmo.
- Pruebas de estrés: Antes de ejecutar un recorrido en un grafo muy grande, es recomendable realizar pruebas de estrés con grafos más pequeños que puedan simular el comportamiento del algoritmo con un tamaño mayor.
- Logs y alertas: Utilizar logs detallados que registren el progreso del recorrido y generen alertas cuando se alcanza un umbral crítico de memoria es otra forma de detectar de manera proactiva un posible problema de sobrecarga.
Una vez detectado un problema de sobrecarga de memoria, existen varias estrategias que se pueden implementar para reducir el impacto y optimizar el algoritmo.
Estrategias para resolver la sobrecarga de memoria:
- Utilización de algoritmos en disco: En lugar de cargar todo el grafo en la memoria, algunos algoritmos, como external memory algorithms, utilizan el almacenamiento en disco para procesar el grafo en partes. Aunque este enfoque puede ser más lento debido al acceso a disco, permite manejar grafos que exceden la capacidad de la RAM.
- Algoritmos de recorrido en streaming: En lugar de almacenar todo el grafo en memoria, los algoritmos en streaming procesan solo una parte del grafo a la vez. Por ejemplo, el recorrido en BFS en streaming procesa cada nivel del grafo por separado, lo que reduce considerablemente la carga de memoria.
- Optimización de estructuras de datos: Cambiar las estructuras de datos subyacentes a otras más eficientes en términos de memoria puede marcar una gran diferencia. Por ejemplo, el uso de matrices de adyacencia dispersas en lugar de matrices densas puede ahorrar una cantidad considerable de memoria en grafos grandes y esparcidos.
- Compresión del grafo: Para reducir la memoria ocupada por los nodos y aristas, se puede aplicar compresión. Las técnicas de compresión, como WebGraph en grafos web, permiten representar el grafo de forma compacta sin perder información esencial para los algoritmos de recorrido.
- Recorridos paralelizados: Utilizar algoritmos paralelizados que dividan el grafo en subgrafos más pequeños y distribuyan la carga entre múltiples núcleos o máquinas puede ayudar a reducir la memoria consumida por cada proceso individual.
Además de las soluciones mencionadas, es importante tener en cuenta el tipo de grafo con el que se está trabajando. Algunos tipos de grafos, como los grafos esparcidos o grafos de redes sociales, pueden presentar patrones que permiten implementar heurísticas o técnicas especializadas para optimizar tanto la memoria como el tiempo de ejecución.
Comparativa de técnicas para manejar la sobrecarga de memoria en grafos grandes:
| Técnica | Ventajas | Desventajas |
|---|---|---|
| External Memory Algorithms | Permiten procesar grafos más grandes que la RAM disponible | Acceso a disco más lento que a memoria RAM |
| Recorridos en Streaming | Reducción significativa de uso de memoria al procesar por partes | Requiere particionar el grafo, lo que puede ser complejo |
| Optimización de Estructuras de Datos | Reducción directa del uso de memoria | No siempre es suficiente en grafos extremadamente grandes |
| Compresión del Grafo | Reduce drásticamente el espacio requerido | Puede aumentar la complejidad de los algoritmos |
| Paralelización | Mejora tanto el tiempo de ejecución como el uso de recursos | Requiere infraestructura paralela o distribuida |
El manejo de la memoria en recorridos de grafos muy grandes es un desafío importante. Sin embargo, con las estrategias adecuadas, es posible resolver este problema y optimizar tanto el uso de memoria como el rendimiento general de los algoritmos de recorrido. Al detectar y abordar estos problemas de manera proactiva, se pueden prevenir sobrecargas críticas en sistemas con recursos limitados.
Heurísticas y Recorridos A* en Grafos**
Los recorridos de grafos son fundamentales en muchos campos, como la inteligencia artificial, la teoría de grafos, y el diseño de sistemas optimizados. Para mejorar la eficiencia de los algoritmos de búsqueda, se utilizan heurísticas, especialmente en algoritmos como el A*, que combina las ventajas de la búsqueda en amplitud (**BFS**) y la búsqueda con costo uniforme. En esta sección, analizaremos qué son las heurísticas y cómo se aplican en algoritmos como el A*.
¿Qué son las heurísticas en los recorridos de grafos?
En el contexto de los recorridos de grafos, las heurísticas son funciones que estiman el costo o la distancia desde un nodo actual hasta el nodo objetivo o meta. Estas estimaciones permiten que los algoritmos de búsqueda tomen decisiones más inteligentes y enfocadas, en lugar de explorar todos los posibles caminos indiscriminadamente. El propósito de una heurística es guiar la búsqueda hacia soluciones más rápidas o eficientes, reduciendo el número de nodos que se exploran durante el proceso.
Una buena heurística debe cumplir dos características principales:
- Admisibilidad: La heurística nunca debe sobreestimar el costo restante para alcanzar el objetivo. Esto asegura que el algoritmo encontrará la solución óptima si existe una.
- Consistencia (o Monótona): El costo estimado por la heurística debe cumplir con la desigualdad triangular, es decir, la estimación del costo desde el nodo actual a cualquier nodo vecino debe ser menor o igual al costo directo desde el nodo vecino al objetivo.
Un ejemplo clásico de una heurística es la distancia euclidiana o la distancia Manhattan en un tablero de ajedrez, que estima la distancia entre dos casillas en función del número de movimientos requeridos.
Ejemplo de funciones heurísticas comunes:
- Distancia Euclidiana: Se utiliza en grafos donde el costo es la distancia física, y se calcula como la distancia recta entre dos puntos.
- Distancia Manhattan: Es ideal para grafos que están en una cuadrícula (como los laberintos), donde solo se pueden hacer movimientos en líneas rectas.
- Heurística personalizada: En ciertos problemas, como los juegos de estrategia, es posible diseñar heurísticas específicas que tomen en cuenta reglas o restricciones del problema en particular.
¿Cómo se usan las heurísticas en algoritmos como A*?
El algoritmo A* es un algoritmo de búsqueda que utiliza una combinación de heurísticas y el costo real de llegar a un nodo. Es ampliamente utilizado en problemas como la navegación de robots, la búsqueda de rutas en videojuegos y la planificación de rutas en mapas. A* se destaca porque utiliza una función de evaluación que combina el costo acumulado para llegar a un nodo y una heurística que estima el costo restante.
La función de evaluación en A* se define como:
f(n) = g(n) + h(n)
- g(n): Representa el costo acumulado desde el nodo inicial hasta el nodo actual n.
- h(n): Es la heurística, que estima el costo desde el nodo actual n hasta el objetivo.
- f(n): Es la suma de ambos costos (costo real más estimación), que determina la prioridad del nodo para su exploración.
El algoritmo A* selecciona el nodo con el valor más bajo de f(n) para explorarlo a continuación. Esto asegura que A* siga el camino que parece más prometedor en función de los costos acumulados y la estimación restante.
Proceso paso a paso del algoritmo A*:
- Inicialización: Se comienza en el nodo inicial, y se asigna a este nodo un valor de g(n) = 0 y f(n) = h(n). El nodo inicial se coloca en una cola de prioridad.
- Expansión de nodos: Se selecciona el nodo con el valor más bajo de f(n) de la cola de prioridad. Este nodo es el que se expandirá explorando sus vecinos.
- Actualización de costos: Para cada nodo vecino, se calcula el nuevo valor de g(n) (suma del costo actual más el costo de moverse al vecino) y se actualiza su valor de f(n).
- Verificación del objetivo: Si se llega al nodo objetivo, el algoritmo termina y devuelve el camino encontrado. Si no, se repite el proceso.
El uso de heurísticas en A* es lo que lo hace mucho más eficiente que otros algoritmos de búsqueda no informados como BFS o DFS, ya que dirige la búsqueda hacia el objetivo de manera más rápida. Mientras que BFS explora todos los nodos a un nivel antes de pasar al siguiente, A* utiliza la heurística para saltar a los nodos más prometedores primero.
Comparativa entre A* y otros algoritmos de búsqueda:
| Algoritmo | Ventajas | Desventajas |
|---|---|---|
| A* | Combina lo mejor de BFS y Dijkstra, encuentra rutas óptimas y es más eficiente gracias a la heurística. | Puede ser costoso en memoria, especialmente si el grafo es muy grande. |
| BFS | Encuentra el camino más corto si todos los costos de los bordes son iguales. | No es eficiente cuando se trabaja con grafos grandes o con costos variables. |
| DFS | Requiere menos memoria que BFS y puede ser útil en grafos muy profundos. | No garantiza encontrar el camino más corto y puede explorar caminos irrelevantes. |
| Dijkstra | Encuentra el camino más corto en grafos ponderados. | No utiliza heurísticas, lo que lo hace más lento que A* en ciertos escenarios. |
Las heurísticas son esenciales para mejorar la eficiencia en la búsqueda de caminos en grafos, especialmente en algoritmos como A*. El uso adecuado de las heurísticas permite que el algoritmo tome decisiones más informadas y se enfoque en los caminos que tienen mayor probabilidad de llevar al objetivo de manera más rápida y con menos consumo de recursos. La elección de la heurística correcta es clave para el éxito del algoritmo en aplicaciones reales.
Si quieres conocer otros artículos parecidos a GRAFOS: Guía-> Recorridos, Profundidad, Anchura y Más puedes visitar la categoría Programación.

Entradas Relacionadas 👇👇