Proyección equidistante: Representación bidimensional de la Tierra con unidades lineales
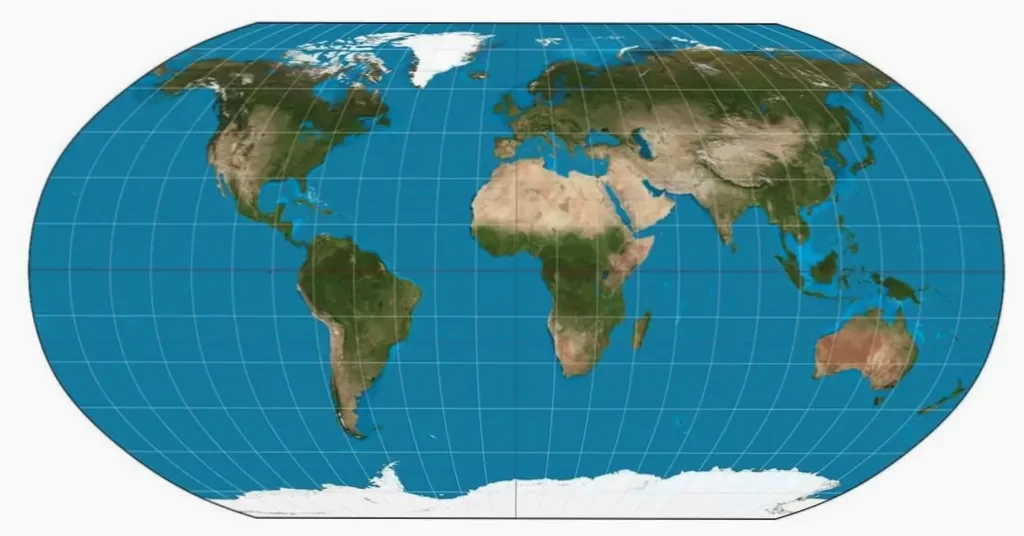
La representación de nuestra realidad tridimensional en un plano bidimensional es un reto que ha inquietado a cartógrafos y matemáticos durante siglos.
Entre las diversas formas de proyectar la Tierra en una superficie plana, la proyección equidistante se destaca por su capacidad para preservar las distancias y ángulos, brindando una herramienta valiosa para la navegación, la planificación urbana y la comprensión de la geopolítica.
¿Qué es la proyección equidistante?
La proyección equidistante es un sistema de coordenadas proyectadas que se utiliza para representar la superficie terrestre en un plano bidimensional.
Esta proyección permite convertir las coordenadas geográficas de longitud y latitud en coordenadas cartesianas x e y, lo que facilita cálculos de distancia y área.
La proyección equidistante es un tipo de proyección cilíndrica, que se caracteriza por mantener las distancias y ángulos entre los objetos en la superficie terrestre.
Esto significa que las longitudes y latitudes se convierten en coordenadas x e y en la proyección plana, manteniendo la relación entre las distancias y ángulos originales.
La proyección equidistante se utiliza en una variedad de aplicaciones, como la cartografía, la navegación, la geografía y la planificación urbana.
Es especialmente útil cuando se requiere una representación precisa de la superficie terrestre en un plano bidimensional.
Entre los beneficios de la proyección equidistante se incluyen:
- Distancias precisas: La proyección equidistante mantiene las distancias entre los objetos en la superficie terrestre, lo que la hace ideal para aplicaciones que requieren cálculos de distancia precisos.
- Ángulos precisos: La proyección equidistante también mantiene los ángulos entre los objetos en la superficie terrestre, lo que es útil para aplicaciones que requieren una representación precisa de la orientación y la dirección.
- Fácil de utilizar: La proyección equidistante es fácil de utilizar y entender, ya que utiliza coordenadas cartesianas x e y que son familiares para muchos usuarios.
La proyección equidistante es un sistema de coordenadas proyectadas que permite representar la superficie terrestre en un plano bidimensional, manteniendo las distancias y ángulos originales.
Es una herramienta útil en una variedad de aplicaciones que requieren una representación precisa de la superficie terrestre.
Definición y concepto
La proyección equidistante se define como una proyección cilíndrica que se utiliza para representar la superficie terrestre en un plano bidimensional.
Esta proyección se basa en la idea de convertir las coordenadas geográficas de longitud y latitud en coordenadas cartesianas x e y.
El concepto de proyección equidistante se basa en la necesidad de representar la superficie terrestre en un plano bidimensional, manteniendo las distancias y ángulos originales.
Esto se logra mediante la utilización de una fórmula matemática que relaciona las coordenadas geográficas con las coordenadas cartesianas.
La fórmula utilizada para la proyección equidistante es la siguiente:
x = R * λ * cos(φ) y = R * φ
Donde:
- x es la coordenada x en la proyección plana
- y es la coordenada y en la proyección plana
- R es el radio de la Tierra
- λ es la longitud geográfica
- φ es la latitud geográfica
Esta fórmula permite convertir las coordenadas geográficas en coordenadas cartesianas, manteniendo las distancias y ángulos originales.
La proyección equidistante es un sistema de coordenadas proyectadas que se utiliza para representar la superficie terrestre en un plano bidimensional, manteniendo las distancias y ángulos originales.
Se basa en la idea de convertir las coordenadas geográficas en coordenadas cartesianas mediante una fórmula matemática.
Ventajas y desventajas de la proyección equidistante
Ventajas de la proyección equidistante
La proyección equidistante ofrece varias ventajas que la convierten en una herramienta útil para la representación bidimensional de la Tierra.
A continuación, se presentan algunas de las ventajas más destacadas:
La proyección equidistante es una representación precisa de la Tierra, ya que mantiene las distancias y ángulos entre los objetos en la superficie terrestre.
Esto la hace ideal para aplicaciones que requieren mediciones precisas, como la navegación aérea o la planificación urbana.
Otra ventaja de la proyección equidistante es que es fácil de calcular y visualizar.
Los cálculos de distancia y área se simplifican gracias a la representación plana, lo que la hace más accesible para los no expertos en cartografía.
La proyección equidistante también es escalable, lo que significa que se puede utilizar para representar áreas pequeñas o grandes con la misma precisión.
Esto la hace ideal para aplicaciones que requieren una gran cantidad de detalles, como la planificación de infraestructuras o la gestión de recursos naturales.
Otra ventaja de la proyección equidistante es que es compatible con la mayoría de los sistemas de información geográfica (SIG) y software de diseño asistido por computadora (CAD).
Esto la hace fácil de integrar en workflows existentes y de compartir información con otros profesionales.
Por último, la proyección equidistante es una herramienta versátil que se puede utilizar en una variedad de disciplinas, como la geografía, la geología, la ingeniería, la arquitectura y la planificación urbana.
Desventajas de la proyección equidistante
Aunque la proyección equidistante ofrece muchas ventajas, también tiene algunas desventajas que es importante considerar.
A continuación, se presentan algunas de las desventajas más destacadas:
Una de las principales desventajas de la proyección equidistante es que no es una representación perfecta de la Tierra.
La Tierra es un cuerpo esférico, y la proyección equidistante no puede capturar completamente su curvatura.
Esto puede llevar a errores en la representación de áreas y distancias en las regiones polares.
Otra desventaja de la proyección equidistante es que no es adecuada para representar grandes áreas.
A medida que se aleja del ecuador, la distorsión en la forma de la Tierra se vuelve más pronunciada, lo que puede llevar a errores en la representación de la realidad.
La proyección equidistante también puede ser limitada en su capacidad para representar características naturales, como montañas, valles y ríos.
Esto se debe a que la proyección equidistante se basa en la representación de la Tierra como un plano, lo que no siempre refleja la complejidad del relieve terrestre.
Otra desventaja de la proyección equidistante es que no es compatible con todas las proyecciones cartográficas.
Esto puede crear problemas al intentar combinar datos de diferentes fuentes o al intentar utilizar la proyección equidistante con otros sistemas de coordenadas.
Por último, la proyección equidistante puede requerir una gran cantidad de recursos computacionales para ser procesada y visualizada.
Esto puede ser un problema para aquellos que trabajan con equipos o software limitados.
La proyección equidistante es una herramienta útil para la representación bidimensional de la Tierra, pero también tiene sus limitaciones.
Es importante considerar cuidadosamente las ventajas y desventajas antes de elegir esta proyección para un proyecto específico.
Aplicaciones de la proyección equidistante
La proyección equidistante tiene una variedad de aplicaciones prácticas en diferentes campos, desde la cartografía hasta la navegación y otras áreas.
A continuación, se presentan algunas de las aplicaciones más importantes de esta proyección.
Uso en la cartografía
En la cartografía, la proyección equidistante se utiliza para crear mapas que muestran la relación entre la latitud y la longitud geográficas y las coordenadas x e y en la proyección plana.
Esto permite a los cartógrafos crear mapas precisos y detallados que muestran la relación entre las diferentes características geográficas, como montañas, ríos y fronteras.
La proyección equidistante es particularmente útil en la creación de mapas temáticos, que muestran la distribución de diferentes variables, como la población, la temperatura, la precipitación, entre otras.
Al utilizar la proyección equidistante, los cartógrafos pueden crear mapas que muestran la relación entre estas variables y la geografía.
Por ejemplo, un mapa que muestra la distribución de la población en una región puede utilizar la proyección equidistante para mostrar la relación entre la población y la geografía, permitiendo a los usuarios visualizar la relación entre la población y las características geográficas, como los ríos, las montañas y las fronteras.
Uso en la navegación
En la navegación, la proyección equidistante se utiliza para determinar la posición y la ruta de un objeto en movimiento, como un barco o un avión.
Al utilizar la proyección equidistante, los navegantes pueden determinar la posición actual y la ruta óptima para llegar a un destino.
Por ejemplo, un navegador puede utilizar la proyección equidistante para determinar la posición actual de un barco en el mar.
Al conocer la latitud y la longitud geográficas, el navegador puede utilizar la proyección equidistante para convertir estas coordenadas en coordenadas x e y en la proyección plana, lo que permite determinar la posición actual del barco.
Además, la proyección equidistante se utiliza en la navegación para determinar la ruta óptima entre dos puntos.
Al utilizar la proyección equidistante, los navegantes pueden determinar la ruta más corta y segura entre dos puntos, lo que reduce el tiempo de viaje y minimiza el riesgo de errores de navegación.
Otras aplicaciones prácticas
La proyección equidistante también tiene otras aplicaciones prácticas en diferentes campos, como la agrimensura, la planificación urbana y la geología.
En la agrimensura, la proyección equidistante se utiliza para determinar la superficie y la forma de los terrenos.
Al utilizar la proyección equidistante, los agrimensores pueden determinar la superficie y la forma de los terrenos con precisión, lo que permite una planificación más efectiva de la tierra.
En la planificación urbana, la proyección equidistante se utiliza para diseñar y planificar ciudades y comunidades.
Al utilizar la proyección equidistante, los planificadores urbanos pueden diseñar y planificar ciudades y comunidades de manera más efectiva, lo que permite una mejor utilización del espacio y una mayor eficiencia en la planificación.
En la geología, la proyección equidistante se utiliza para determinar la forma y la estructura de los terrenos.
Al utilizar la proyección equidistante, los geólogos pueden determinar la forma y la estructura de los terrenos con precisión, lo que permite una mejor comprensión de la estructura geológica de la Tierra.
La proyección equidistante tiene una variedad de aplicaciones prácticas en diferentes campos, desde la cartografía hasta la navegación y otras áreas.
Su capacidad para convertir coordenadas geográficas en coordenadas planas hace que sea una herramienta valiosa para una variedad de propósitos.
| Aplicación | Descripción |
|---|---|
| Cartografía | Crear mapas precisos y detallados que muestran la relación entre la latitud y la longitud geográficas y las coordenadas x e y en la proyección plana. |
| Navegación | Determinar la posición y la ruta de un objeto en movimiento, como un barco o un avión. |
| Agrimensura | Determinar la superficie y la forma de los terrenos. |
| Planificación urbana | Diseñar y planificar ciudades y comunidades de manera más efectiva. |
| Geología | Determinar la forma y la estructura de los terrenos. |
La proyección equidistante es una herramienta valiosa que tiene una variedad de aplicaciones prácticas en diferentes campos.
Su capacidad para convertir coordenadas geográficas en coordenadas planas hace que sea una herramienta fundamental en la cartografía, la navegación y otras áreas.
Tipo de proyecciones equidistantes
Las proyecciones equidistantes son una familia de proyecciones cartográficas que intentan representar la superficie curva de la Tierra en una superficie plana, manteniendo la relación de distancias entre los puntos.
Existen varias variedades de proyecciones equidistantes, cada una con sus características y aplicaciones específicas.
Dentro de las proyecciones equidistantes, podemos distinguir dos tipos principales: proyecciones azimutales y proyecciones cilíndricas.
Estas dos categorías se basan en la forma en que se proyectan los puntos de la Tierra en una superficie plana.
Las proyecciones equidistantes tienen la ventaja de preservar las distancias entre los puntos, lo que las hace ideales para aplicaciones que requieren medir distancias precisas, como la navegación aérea o marítima.
Proyección equidistante azimutal
La proyección equidistante azimutal, también conocida como proyección azimutal equidistante, es una proyección cartográfica que proyecta los puntos de la Tierra en una superficie plana, manteniendo la relación de distancias entre los puntos.
En esta proyección, los puntos se proyectan desde el centro de la Tierra, lo que significa que la distancia entre dos puntos en la proyección es proporcional a la distancia real entre ellos en la superficie de la Tierra.
La proyección equidistante azimutal es útil para representar áreas pequeñas, como ciudades o regiones, ya que mantiene la relación de distancias entre los puntos y es fácil de interpretar.
Una de las ventajas de la proyección equidistante azimutal es que es fácil de calcular, ya que solo se requiere la latitud y longitud de los puntos para determinar su posición en la proyección.
Sin embargo, la proyección equidistante azimutal no es adecuada para representar áreas grandes, ya que la distorsión aumenta con la distancia del centro de la proyección.
Proyección equidistante cilíndrica
La proyección equidistante cilíndrica es una proyección cartográfica que proyecta los puntos de la Tierra en una superficie cilíndrica y luego la desenrolla en una superficie plana.
En esta proyección, los paralelos se representan como líneas rectas y los meridianos se representan como líneas curvas.
La proyección equidistante cilíndrica es útil para representar áreas grandes, como continentes o países, ya que mantiene la relación de distancias entre los puntos y es fácil de interpretar.
Una de las ventajas de la proyección equidistante cilíndrica es que es adecuada para representar áreas grandes, ya que la distorsión es menor que en la proyección azimutal.
Sin embargo, la proyección equidistante cilíndrica puede ser más difícil de calcular que la proyección azimutal, ya que requiere la latitud y longitud de los puntos, así como la relación entre la superficie cilíndrica y la superficie plana.
Otras variedades de proyecciones equidistantes
Además de las proyecciones azimutales y cilíndricas, existen otras variedades de proyecciones equidistantes, como la proyección de Gall-Peters, la proyección de Winkel tripel y la proyección de Eckert IV.
La proyección de Gall-Peters es una proyección cilíndrica que intenta reducir la distorsión en la representación de áreas y formas.
La proyección de Winkel tripel es una proyección azimutal que combina la proyección azimutal equidistante con la proyección cilíndrica, lo que la hace adecuada para representar áreas grandes y pequeñas.
La proyección de Eckert IV es una proyección cilíndrica que intenta reducir la distorsión en la representación de áreas y formas, y es adecuada para representar áreas grandes.
Las proyecciones equidistantes son una familia de proyecciones cartográficas que intentan representar la superficie curva de la Tierra en una superficie plana, manteniendo la relación de distancias entre los puntos.
Existiendo varias variedades, cada una con sus características y aplicaciones específicas.
História de la proyección equidistante
La proyección equidistante es un sistema de coordenadas proyectadas que se remonta al siglo XVI, cuando los cartógrafos comenzaron a buscar formas de representar la Tierra de manera bidimensional y precisa.
Uno de los precursores de esta técnica fue el matemático y astrónomo alemán Johannes Werner, quien en 1514 publicó un tratado sobre la proyección estereográfica, un método que se basa en la proyección de la esfera terrestre sobre un plano tangente.
En el siglo XVII, el matemático y astrónomo holandés Willebrord Snellius desarrolló un método para proyectar la esfera terrestre sobre un plano, lo que se conoció como la "proyección de Snellius".
Esta proyección se basaba en la idea de dividir la esfera en pequeñas secciones y luego proyectarlas sobre un plano.
En el siglo XVIII, el matemático y astrónomo francés Joseph-Louis Lagrange desarrolló una proyección más precisa conocida como la "proyección de Lagrange", que se basaba en la teoría de la proyección estereográfica.
Esta proyección se utilizó ampliamente en la cartografía y la navegación durante siglos.
Orígenes y desarrollo
La proyección equidistante como la conocemos hoy en día se desarrolló en el siglo XIX, cuando los cartógrafos y matemáticos comenzaron a buscar formas de representar la Tierra de manera más precisa y detallada.
Uno de los pioneros en este campo fue el cartógrafo alemán Carl Friedrich Gauss, quien en 1824 publicó un tratado sobre la proyección gaussiana, que se basaba en la teoría de la proyección estereográfica.
En la segunda mitad del siglo XIX, la proyección equidistante se convirtió en un estándar en la cartografía, ya que permitía representar la Tierra de manera precisa y detallada, lo que fue fundamental para la navegación y la exploración.
En el siglo XX, la proyección equidistante se perfeccionó con el desarrollo de la teoría de la proyección conforme, que se basa en la idea de preservar las formas y las distancias en la proyección.
Esta teoría permitió la creación de mapas más precisos y detallados.
Contribuciones destacadas
Una de las contribuciones más destacadas en el desarrollo de la proyección equidistante fue la del matemático y astrónomo estadounidense John Paul Goode, quien en 1923 publicó un tratado sobre la proyección homoloidal, que se basaba en la teoría de la proyección conforme.
Otra contribución destacada fue la del cartógrafo y matemático soviético Vladimir Vasilievich Kavrayskiy, quien en 1934 desarrolló la proyección de Kavrayskiy, que se basaba en la teoría de la proyección estereográfica.
En la segunda mitad del siglo XX, la proyección equidistante se volvió más precisa y detallada con el desarrollo de la tecnología de los sistemas de información geográfica (SIG), que permitió la creación de mapas digitales y la representación de la Tierra de manera más precisa.
Si quieres conocer otros artículos parecidos a Proyección equidistante: Representación bidimensional de la Tierra con unidades lineales puedes visitar la categoría Tecnología.

Entradas Relacionadas 👇👇